2000年度森泰吉郎記念研究振興基金「国際共同研究」報告書

2000年度森泰吉郎記念研究振興基金「国際共同研究」
概念階層と概念記述の相互学習による漸増学習について

～関連研究調査～

本研究テーマでは，帰納論理プログラミング(ILP)における概念階層の構築・更新・利用や，学習における言語バイアスの動的な変更，及び事例間の類似度に関して研究を行う必要がある．本関連研究調査報告書では，これらの観点から，特に関連の深いと思われる論文に関する調査結果を示す．

Contents

Yamazaki, T., Pazzani, M. J., and Merz, C.:
Acquiring and updating hierarchical knowledge for machine translation based on a clustering technique,
In Wermter, Riloff & Scheler (Eds.) Connectionist, Statistical, and Symbolic Approaches to Learning for Natural Language Processing, 1996.

Khan, K., Muggleton, S. and Parson, R.:
Repeat learning using predicate invention,
In C.D. Page, editor, Proc. of the 8th International Workshop on Inductive Logic Programming (ILP-98), LNAI 1446, pages 165-174, Berlin, 1998. Springer-Verlag.

森中雄, 大原剛三, 馬場口登，北橋忠宏:
事例関の非類似度を用いたデータベースからのクラス間関係の獲得,
情報処理学会論文誌, Vol.41, No.11, pp.3193-3196, Nov. 2000.

Mitchell, T. M.:
The Role of Unlabeled Data in Supervised Learning,
Proc. of the Sixth International Colloquium on Cognitive Science, 1999.

Yamazaki, T., Pazzani, M. J., and Merz, C.:
Acquiring and updating hierarchical knowledge for machine translation based on a clustering technique,
In Wermter, Riloff & Scheler (Eds.) Connectionist, Statistical, and Symbolic Approaches to Learning for Natural Language Processing, 1996.

この論文は，機械翻訳システムを対象とし，翻訳のためのルールの獲得，及びその獲得に利用される概念階層の生成・更新する方法について述べている．

翻訳のためのルールは，ILPの枠組で獲得される．具体的には，ILPシステム FOCLに，背景知識として与えられる階層構造をより効率良く利用するための拡張を行い，それを利用している．

一方，概念階層の構築・更新は，翻訳のためのルールと(存在する場合は)既存の概念階層を入力とし，クラスタリングの技術を利用して行われる(下図参照)．

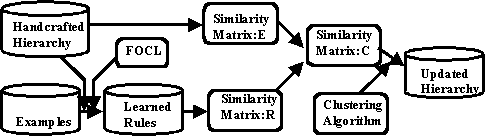
この図は，論文中Fig.3を編集したものである．

Khan, K., Muggleton, S. and Parson, R.:
Repeat learning using predicate invention,
In C.D. Page, editor, Proc. of the 8th International Workshop on Inductive Logic Programming (ILP-98), LNAI 1446, pages 165-174, Berlin, 1998. Springer-Verlag.

述語発明(Predicate Invention, PI)とは，学習に必要な述語(語彙)を(自動的に)発明する手法であり，これまでに数多くの研究が行われている．しかし，これまでの研究では，いつPIが必要になるのか，またどの様に新たな述語を発明するのか，についての言及が多く，実際にPIを行なう事が，学習の向上につながるかどうかは不明な点も多い．すなわち，利用する述語の増大は，仮説空間の増大につながるので，はたして精度や実行効率に良い影響を与えるとは限らないであろう，ということである．

一方，この論文では，ある条件下でのPIの適用可能性について述べている．それは，学習者が(背景知識として利用される)関連する一連の概念の定義を発見するために，PIを繰り返し適用することが許される場合，という条件である．この論文では，以上の条件の下，ある概念の説明に寄与する述語をPIにより導入する事で，後の概念の学習に必要とされる事例数を減らせる可能性がある，ということを，理論的な側面，定量的な評価実験によって示している．

森中雄, 大原剛三, 馬場口登，北橋忠宏:
事例関の非類似度を用いたデータベースからのクラス間関係の獲得,
情報処理学会論文誌, Vol.41, No.11, pp.3193-3196, Nov. 2000.

データベース中に複数のクラスが与えられる場合に，属性値の発生確率を反映した事例関の非類似度を利用して，任意の２クラス間の関係を獲得する手法を与えている．

ここで異なるクラスA,B間のクラス間関係とは，

包含：クラスA中の全事例がクラスBに含まれる

排反：クラスA中のいずれの事例もクラスBに含まれない

一部共有：クラスA中の事例の一部がクラスBに含まれる

のいずれかである．この論文では，以下に示す事例間の非類似度および限界非類似度を利用して，このクラス間関係を獲得する手法が示されている．

事例a,b間の非類似度D(a,b)は以下のように定義される．
D(a,b) = Σ Pk(a)≠ Pk(b) ｛E(Pk(a)) + E(Pk(b)) ｝
ここで

Pk(a)は事例aの k番目の属性値

E(v) = 1+w｛1-H(p)｝ (0 ＜ p(v) ＜ 1 )
E(v) = ∞ (p(v) = 0,1)

p(v)は属性Pにおける属性値vの発生確率

wは発生確率を非類似度に反映させる重み

H(p) = -p log(p) - (1-p) log(1-p)

である．
さらに，クラスCに属する事例集合を｛ a1, a2, ．．． an ｝とするとき，Cの限界非類似度DL(C) は，以下のように定義される．

DL(C) = max [ min ｛ D(ai,aj) ｝]

i=1,2,..,n j=1,2,..,n (i≠j)

提案手法は，扱えるデータの形式を属性 = 値表に限定したものであり，扱える問題のクラスは命題論理学習器で扱う問題クラスを前提としている．しかし，以下に示す，これまでに提案されている一階述語論理上での類似性や距離などの概念を用いれば，述語論理で表現されるデータベースからのクラス間関係の獲得も可能であると考えられる．

Mitchell, T. M.:
The Role of Unlabeled Data in Supervised Learning,
Proc. of the Sixth International Colloquium on Cognitive Science, 1999.

データマイニングや決定木の生成，帰納論理プログラミングなどの教師付き学習の計算モデルでは予めクラス分けされた訓練事例を利用し，クラス分けされていない訓練事例が持ちうる役割を無視している．

一方，この論文では，教師付き学習におけるクラス分けされていない訓練事例の潜在的な役割について述べられている．クラス分けされていないデータを利用するためのアルゴリズム'' Cotrainingアルゴリズム''が示され， Cotrainingアルゴリズムが適用可能である問題のクラスとして，「例を表す特徴が分類に冗長に十分な(redundantly sufficient)である」，というクラスが導入されている．さらにWebページの分類問題を例にクラス分けされていないデータの利用が，学習精度の向上につながることを実験により示している．

Web pageの分類問題におけるCotrainingアルゴリズム
Given

set L of labeled training examples

set U of unlabeled examples

Loop:

Learn hyperlink-based classifier H from L

Learn full-text classifier F from L

Allow H to label p positive and n negative examples from U

Allow F to label p positive and n negative examples from U

Add these self-labeled examples to L

また論文中で述べられている通り，この手法は，人間が直面する言語獲得や物体の認識などにも有効であると考えられる．

その他の関連論文リスト

 ILPにおける概念階層や型階層の利用に関する関連論文

A.M. Frisch, A.M.: Sorted Downward Refinement: Building Background Knowledge into a Refinement Operator for Inductive Logic Programming. Proc. of the 9th International Workshop on Inductive Logic programming, pp.104-115, 199.

石川孝, 美宅成樹, 寺野隆雄: 概念階層と探索バイアスを用いたILP手法によるタンパク質機能モデルの発見, 人工知能学会誌, Vol. 15, No. 1, pp. 169-178, 2000.

佐々木裕: 型付き論理プログラムの正例からの学習, 人工知能学会誌, Vol.15, No.1, pp.147-154, 2000.

Sasaki, Y., and Haruno, M.: RHB+: A Type-Oriented ILP System Learning from Positive Data, Proc. of the 15th International Conference on Artificial Intelligence, pp.894-899, 1997.

Sommer, E., Emde, W., Kietz, J.-U. and Wrobel, S.: MOBAL User Guide, 1996.

一階述語論理におけるクラスタリングアルゴリズムに関する関連論文

Bisson, G.: Conceptual Clustering in a First-Order Logic Representation, Proc. of the 10th European Conference on Artificial Intelligence, pp.458-462, 1992.

Blockeel, H., De Raedt, L. and Ramon, J.: Top-down induction of clustering trees, Proc. of the 15th International Conference on Machine Learning, pp.55-63, 1998.

Emde, W.: Inductive learning of characteristic concept descriptions from small set of classified examples, Proc. of the 7th European Conference on Machine Learning, pp.103-121, 1994.

Kirsten, M. and Wrobel, S.: Relational distance-based clustering, Proc. of the 8th International Conference on Inductive Logic programming, pp.261-270, 1998,

Kirsten, M. and Wrobel, S.: Estending K-Menas Clustering to First-Order Representations, Proc. of the 10th International Conference on Inductive Logic Programming, pp.112-129, 2000.

バイアスシフト・述語発明に関する関連論文

Bain, M. and Muggleton, S.: Non-monotonic learning, Inductive Logic Programming, Academic Press, 1992.

Kijsirikul, B., Numao, M, and Shimura, M.: Discrimination-based constructive induction of logic programming, Proc. of the 10th National Conference on Artificial Intelligence, 1992.

Lapointe S., Ling, C. and Matwin, S.: Constructive Inductive Logic programming, Proc. of the 16th International Joint conference on Artificial Intelligence, pp.1030-1036, 1993.

Lavrac, N. Gamberger, D. and Turney, P.: A relevancy filter for constructive induction, IEEE Intelligent Systems, 13(2), pp.50-56, March-April,1998.

Ling, C.: Inventing necessary theoretical terms in scientific discovery and inductive logic programming, Technical Report 302, Dept. of Comp. Sci., Univ. of Western Ontario, 1991

Martin, L. and Vrain, C. Systematic Predicate Invention in Inductive Logic Programming, Proc. of the 7th International Workshop on Inductive Logic Programming, pp.189-204, 1997.

Muggleton, S.: Duce, an oracle based approach to constructive induction, Proc. of the 10th International Joint Conference on Artificial Intelligence, pp.287-292, 1987.

Muggleton, S.: A strategy for constructing new predicates in first order logic, Proc. of the 3rd European Working Session on Learning, pp.123-130, 1988.

Muggleton, S. and Buntine, W.: Machine invention of first-order predicates by inverting resolution, Proc. of the 5th International Conference on Machine Learning, pp.339-352, 1988.

Muggleton, S.: Predicate invention and utilisation, Journal of Experimental and Theoretical Artificial Intelligence, 6(1),pp.127-130, 1994.

Stahl, I.: Constructive induction in inductive logic programming: an overview, Technical report, Fakultat Informatik, Universitat Stuttgart, 1992.

Stahl, I.: The Efficiency of Bias Shift Operations in ILP. Proc. of the 5th International Workshop on Inductive Logic Programming,pp.231-246,1995.

Stahl, I.: The appropriateness of predicate invention as bias shift operation in ILP, Machine Learning, 20(1/2),pp.95-118, 1995.

Stahl, I.: Predicate invention in inductive logic programming, In L. De Raedt (ed.), Advances in Inductive Logic Programming, pp.34-47, IOS Press, Ohmsha, Amsterdam, 1996.

Srinivasan, A. and King, R.: Feature construction with Inductive Logic Programming: a study of quantitative predictions of biological activity aided by structural attributes, Data Mining and Knowledge Discovery, 3(1),pp.37-57, 1999.

Wirth, R. and O'Rorke, P.: Constraints on predicate invention, Proc. of the 8th International Workshop on Machine Learning, pp.457-461, 1991.

Wrobel, S.: Concept formation during interactive theory revision, Machine Learning Journal, Vol.14, pp.169-191, 1994.

一階述語論理における類似性・距離に関する関連論文

Bisson, G.: Learning FOL with a similarity measure, Proc. of the 10th AAAI, 1992.

Emde, W. and Wettscherek, D.: Relational instance based learning, Proc. of ICML-96, pp.122-130, 1996.

Horvath, T., Wrobel, S. and Bohnebeck, U.: Term comparisons in first-order similarity measures, Proc. of the 8th International Conference on Inductive Logic Programming, pp.65-79, 1998.

Hutchinson, A.: Pseudo-Metrics on Terms and Clauses, Proc. of the 9th European Conference on Machine Learning, 1997.

Nienhuys-Cheng, S.-H.: Distance Between Herbrand Interpretations: A Measure for Approximations to a Target Concept. Proc. of the 7th International Workshop on Inductive Logic Programming, pp.213-226, 1997,

Nienhuys-Cheng, S.-H.: Distances and Limits on Herbrand Interpretations, Proc. of the 8th International Workshop on Inductive Logic Programming, pp.250-260, 1998.

Ramon, J. Bruynooghe, M.: A framework for difining distances between first-order logic objects, Proc. of the 8th International Conference on Inductive Logic Programming, pp,271-280, 1998.

Sebag, M.: Distance Induction in First Order Logic, Proc. of the 7th International Workshop on Inductive Logic Programming, LNAI 1297, pp.264-272, Springer, 1997.

DL(C) =	max [ min ｛ D(ai,aj) ｝]
	i=1,2,..,n j=1,2,..,n (i≠j)