共感覚のÒ美しい音Óの定義付けとその合成に関しての研究
政策メディア研究科 修士2年
花野井俊介
<概要>
我々が普段耳にしている音に対して、各個人の感覚に基づいた解釈が行われていると考えられる。その中の、グラスハーモニカ、グラスハープについての音がどのように歴史的に捉えられて来たのか、またどのような音を生成しているのかを調査する。
ワイングラス内に水を入れ、そのグラスのふちを擦ることで美しい音が発生するという事は昔から知られている。これはグラスハープと呼ばれている。そしてこのワイングラスの振動モードに関する研究や、その物理現象をフィジカルモデリングで再現する研究も進んでいる。しかし、その音の根本的な良さについての研究は抽象的な論議になり、心理学の側面が出てくる。また、このグラスハープを楽器としてベンジャミンフランクリンがアルモニカと呼ばれる楽器を発明した。本研究はそのワイングラスが生み出す音の要素を検証し、どの要素が一般的に言われている、良い音を発生させるのかを、加算合成、クロスシンセシス、FM合成などを用いて検証する。また、その合成で作られた音のどの要素がグラスハープ、グラスハーモニカの音の構成に強く影響を及ぼしているのかを調査する。
序章 はじめに
今日、パーソナルコンピューターの進化によって、以前には不可能とされて来た計算処理が可能になった。その中、コンピューターミュージックにおけるフィジカルモデリング音源の台頭はめざましく、この流れは今後もつづくものと考えられる。しかし、このフィジカルモデリングが用いられる理由は、生楽器に近い音を再現することにある。デジタルでアナログを再現するという流れもある。これらを通常のサンプリング音源と比較すると、システム内での音源調整が容易という点が優れている。実際に商用として用いられているフィジカルモデリング音源を用いた楽器には、YAMAHA社製のエレクトーンや、KORG社製のMOSS音源などがある。これらの音源は今後もより広がっていくと考えられる。しかしながら、音楽を楽しむ上でなぜこれら物理的特徴が良いとされるのかに関しての研究はまだ少ない。本研究ではフィジカルモデリングでも再現され、歴史的にも美しい音とされるグラスハーモニカの音の何が人間の感性に触れるのかを要素ごとに検証をする。
第一章 研究の目的
自分で音を合成する際に、いかに良い音を作るのかは至上の命題である。そしてその良さはどうやって作れば良いのか、そしてどう判断すれば良いのかということに悩み続けて来た。本研究では、自分が良い音だと感じるグラスハーモニカの音を用いてその音がどのように良いと評価されるのかを検証する。つまり、グラスハーモニカの音を構成する要素である、ハーモニーや、エンベロープなどを個別にグラスハーモニカのフィジカルモデルに関してはプログラミング言語Faustなどで再現されている。この音はグラスの物理的特性を再現しているのみで、モデルによっては再現できているとは言い難い。そして、グラスハーモニカが人によって演奏されることで生み出す音の心地よさはどこから来る現象なのかを明確に調査している先攻研究は見つける事ができなかった。そこで本研究ではその調査を加算合成で作成された音とグラスハープを用いて演奏を行っている音楽CDから一部の音を抜き出し、その音の特性を用いて音声合成を行う。そしてどの要素が良い音と感じる重要な要素なのかを特定することで、一般化したモデルを作成する際に注目すべき点がどこにあるかを調査する。
第一節 グラスハープの歴史
グラスハープについての歴史は、弘前大学教育学部紀要にある、冨田による説明が非常に分かりやすくまとめられているのでそれを引用する。
(引用ここから)グラスハープGlassHarpとは、ワイングラスなどの椀形のガラスを水で濡れた指で擦って音を出す楽器である。音の高さの異なる複数のグラスによって楽曲を演奏することができる。音の高さはグラスの大きさなどによって異なり、底面を削ったり、中に水を入れたりすることにより微調整されこともある。歴史上この楽器にはいくつもの呼称がつけられており、ミュージカル・グラスMusicalGlasses、エンジェリック・オルガン(天使のオルガン)AngelicOrgan、セラフィムSeraphim,ヴェリョンVerrillonsなどと呼ばれることもある。複数のグラスを使って音楽を奏でることは中近東などで古くからおこなわれており、ペルシャから11世紀以降に伝えられたものがヨーロッパにおいてミュージカル・グラスとして派生していった。そして17世紀になると、薄手のグラスの縁を濡れた指先でこする奏法が確立されるようになった。当時、科学的嗜好か社交の場での玩具程度にしかみなされていなかったミュージカル・グラスであるが、18世紀の前半には、本格的な音楽演奏にも使われるようになっていった。アイルランド人のリチャード・ポックリッジRichardPuckeridge(1690-1759)は、移動可能なミュージカル・グラスを開発し1742年頃からブリテン諸島各地での演奏をおこなった。「天使のオルガン」AngelicOrganと呼ばれたポックリッジの楽器は、さまざまな大きさのグラスを水で調律するもので、人々から親しまれるとともに、後継者も育ち、1961年には演奏教本も出版された。また1746年、作曲家のグルックChristophWillibaldGluck(1714-1787)は、1746年、ロンドンで「26個のグラスのための協奏曲」を上演している。こうして1950年代からグラスハープはイギリス諸島を中心に高い人気を得るようになっていった。
一方、グラスハープを改良することにより派生した楽器にグラスハーモニカ Glass Harmonica(アルモニカ Armonica)がある。アメリカの政治家であり避雷針の発明などでも有名なベンジャミン・フランクリ(Benjamin Franklin 1706-1790)が1761年に発明したものである。大きさを段階的に変えた複数の椀状ガラスを軸に取り付け、それを足踏みミシンの要領で回転させるもので、奏者は回転するガラスの側面に指を乗せて音を出す。グラスハープでは、一人の奏者が同時に出せる音数は、2・3音程度あり、早いパッセージは演奏しづらいのに対し、グラスハーモニカでは鍵盤楽器のような奏法により、一人の奏者で同時に多くの音を奏でることができ、また、ある程度の早い音の動きにも対応できるようにもなった。そして、グラスハーモニカは上流階級のステータスシンボルとして意味ももつようにもなった。こうしてグラスハーモニカは、18世紀後半のヨーロッパの貴族社会で流行となり、フランス王妃のマリー・アントワネットがこれを習い奏でたほか、モーツァルトもグラスハーモニカのための楽曲を書き下ろした。 グラスハーモニカは、グラスハープの欠点を改善することにより生まれた楽器だが、グラスハープのすべての欠点が克服されたわけではない。グラスハープでは、グラスを擦る指の圧力や速度を奏者が自由に変化させられるので個々の音に表情をつけやすいが、グラスハーモニカでは一定速度で回っているグラスに指先を乗せるので音に表情をつけづらい。また、グラスハープでは、グラスに水を入れれば音に揺らぎが生まれ、また共鳴板や共鳴箱によって音がまろやかになるが、中に水を入れないグラスハーモニカでは音の揺らぎは少なく、構造上、共鳴板や共鳴箱をつけられないので、その音色はどことなく冷たい。つまり、グラスハープとグラスハーモニカはガラスが音を発する原理こそ同じものの、異なった特徴をもった別の種類の楽器である。(引用ここまで)

図1,グラスハープa)

図2, グラスハーモニカb)
グラスハープは歴史的にも長く使用されており、今でも路上でライブ演奏を行っている人を見かける事がある。この、日常的に使用するグラスを楽器として使用する事で手軽に演奏する事が出来るのである。
第二節 先攻研究
グラスハーモニカのフィジカルモデリングに関する研究においては、スタンフォード大学のRomain Michon,
Julius O.Smithらが音楽プログラミング言語Faustを用いて行ったものがある。しかしながら、このソフトウェアが生成する音は打音と弦によって擦った音のモデルであり、奏者が行う指によって生まれるゆらぎが無く、演奏を聞いた経験からこれは似ているとは言い難い。また、グラスハープの振動モードや含まれる倍音成分に関する研究は電気通信大学の、Koichi Uchida、Kenshi Kishiらによると、グラスハープでは振動は柄の影響は受けないこと、音高と音色はグラスの膨らみで変化すること、音高カップの底をカットすることで調整されるということが述べられている。
一方で、グラスハープ、グラスハーモニカ歴史等の研究に関しては多数ある。
グラスハーモニカの研究は倍音成分や振動モードに関する研究が盛んであると同時に、その中心となっている。これは著者が物理的特性の研究か、芸術史やその周辺の研究に分けられていることが考えられる。しかし、流れはベンジャミンフランクリンの発明からであることに変わりはない。
第二章 調査手法
ワイングラスの何が良い音なのかを調べるために、グラスハープだけではなく、その発展系であるグラスハーモニカに関しても調査を行った。構造は中に水を入れるか入れないか、また自動で回転するか否かの違いしか無い。また、初期段階でグラスハープの演奏が
そこで、グラスハーモニカの音を解析しその音が持つ特性、ハーモニー、エンベロープ等を別の複数の音源とコンボリューションを用いて再現する。これはクロスシンセシスと呼ばれ、フォルマント合成を行うものである。
あらかじめ用意した音との合成ではクロスシンセシスを用い、それぞれの音をキャリア音としてエンベロープ成分に関してコンボリューションを行った。FM合成音の加算合成では、まずグラスハーモニカの周波数解析を行い、そのスペクトログラムから必要な周波数を探しだし、サイン波を用いてFM合成を行った上で、それらを加算合成した。それらのエンベロープを個別に変化させる事でより本物らしい音を目指した。これは時変加算合成と呼ばれる。次にそれぞれの要素を調査するための手順を述べる。
なお、調査に用いた音源は、物理的特性が同じ、かつプロフェッショナルが演奏している、という条件から『MEISTER MUSICのアダージョ〜グラスハーモニカ作品集〜 ウィーン・グラスハーモニカ・デュオ』の、『F.シューベルト:アヴェ・マリア』の冒頭グラスハーモニカソロパートの一部、約3秒を用いた。CDのサンプリングレートは44.1khzである。
第一節 グラスハープの周波数解析
先に述べたように、日常的に使用するワイングラスを楽器として使用する事で手軽に美しい音色を出す事ができる、とされているグラスハープであるが、実際これには熟練が必要であり、すぐに美しい音が出るとは限らない。実際にグラスハープを演奏してみたところ、その音のスペクトラムは以下のようになった。(図3)このスペクトラムは、録音の際に発生した低周波部分のノイズを除去するためフィルターを用いている。なお、このスペクトラムは演奏の時間で平均化されたスペクトラムである。そして、15000Hz以上が無いのは音声ファイルのサンプリングレートの問題である。しかし、人間の可聴域は一般的に20Hz〜20000Hzまでであること、そしてそのような高調波や超音波を解析するためには非常に高価な機材が必要なことから、今回は考慮の対象から除外した。スペクトラム表示には描画が分かりやすい理由により、フリーウェアであるAudacityを用いて解析を行った。窓サイズを2048に設定し、対数グラフで表示をした。このグラフはブロック毎に時間平均されている。また、スペクトラムの時間変化を調べるためにソノグラムを用いた。
可聴域以上の音が人間に与える影響は、大橋力によるハイパーソニック・エフェクトの研究などがある。これは、可聴域以上の音(26kHz以上)は皮膚から脳に伝達され、視床の血流が増加する事で脳基幹部を活性化するというものである。そしてこれはこの超音波だけではなく、可聴域部の音が同時に存在するときにだけ、独特の効果が現れてくるというものである。
グラスハープのスペクトラムは整数倍以外の倍音も発生する。Koichi Uchida、Kenshi Kishiらの研究によると、グラスの形状に影響を受けるとしている。グラスの選定がすなわち楽器の質に直結しているのである。グラスハープのスペクトログラム(図4)では、多くの倍音が発生している事が分かる。
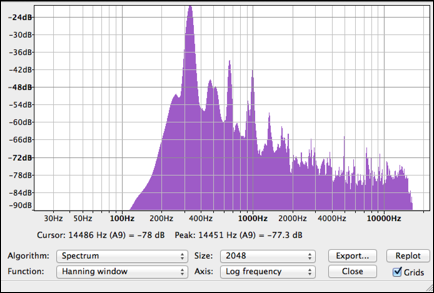
図3, グラスハープのスペクトラム
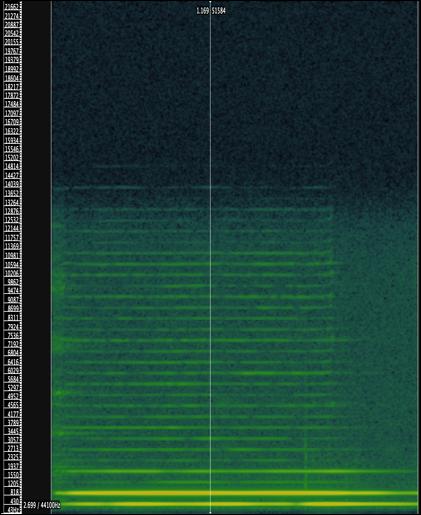
図4, グラスハープのスペクトログラム
第二節 グラスハーモニカの周波数解析
次に、グラスハーモニカが持つスペクトルを分析する。スペクトログラムはフリーウェアであるSonic Visualiserを用い、こちらは倍音の構成とその減衰の様子を見やすくするためにリニア表示をした。(図5,図6)
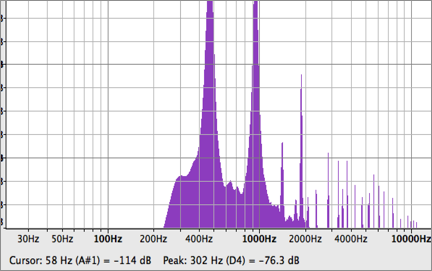
図5. グラスハーモニカのスペクトラム(横軸:周波数、縦軸:音圧)
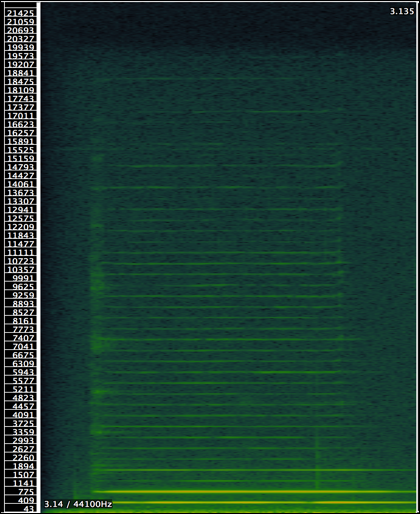
図6 , グラスハーモニカのスペクトログラム(縦軸:周波数、横軸:時間、色濃淡:音圧)
これらのグラフから、グラスハープの倍音は下から基音である469Hzから937Hz、1878Hzとほぼ理論通りに倍音を発生させているが、それ以外の複数の音も同時に発生している。図3のグラフに色をつけて倍音の相関を表したのが次のグラフである。(図5)
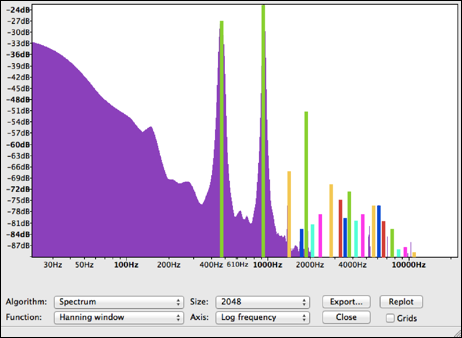
図7, 倍音の相関を色で表示したスペクトラム
このグラフを見ると、複数の倍音が発生している事が分かる。一つの楽器からここまで複数の倍音が発生するという事は極めて異質なことである。これはグラスハープのもつ端の無い形状、つまり周期境界条件が生み出している。周期境界条件とグラスの振動方法に関しては先攻研究が数多くあるが、本研究の意図する点とは方向が異なるため、参照程度に留めることとする。
このような振動は、グラスハーモニカやグラスハープの原理に変わりはない。この振動方法は振動モードと呼ばれ、異なる振動を生み出している。(図6)これによって、同時に複数の倍音が発生することができる。複数の倍音が非整数倍で発生する事で、それぞれことなる整数倍音が干渉していると考えられる。

図8, グラスの振動モード(Koichi Uchida, Kenshi
Kishi, Vubrational analysis
of glass harp and its tone control , The Acoustical Society of Japan,Acoust. Sci. & Tech. 28.6(2007)より引用)
図3、5ともに低域が多く発生している理由はマイクノイズである。よって今回の検証では無視する事とする。
図5におけるオクターブ毎の倍音が似たエンベロープをしているのでは無いのかという仮定のもとで作成した。この組み合わせを表にすると以下のようになる。(表1)斜線は用いた音源ファイルではそれ以上の広域を測定する事が出来なかった。サンプリング周波数の半分の周波数まで理論上は測定できるはずだったので、22000Hzまでを調査する予定だったができなかった。しかしながら、高域ほど減衰が早いことが図4にて確認できたので、今回はそれを無視することとする。
表1 図5を基にしたオクターブ倍音の周波数分布(Hz)
|
色\音 |
基音 |
第1倍音 |
第2倍音 |
第3倍音 |
第4倍音 |
|
緑 |
469 |
937 |
1878 |
3751 |
7502 |
|
黄 |
1405 |
2810 |
5627 |
11246 |
|
|
青 |
1728 |
3512 |
7027 |
|
|
|
水色 |
2064 |
4214 |
8039 |
|
|
|
ピンク |
2340 |
4684 |
9370 |
|
|
|
赤 |
3280 |
6557 |
|
|
|
表1より、ほぼ全ての波は基音の469Hzの倍音になっている。理論通りの倍音が発生している事がわかる。しかし、完全に倍音になっていないという点に注目できる。周波数が近いサイン波が加算合成されると、うなりを生み出すということは広く知られている。これは整数倍音の値が微妙にずれていることからも発生する。
第三節 音圧変化の解析
次に音圧の時間変化を調査する。グラスハーモニカのオーディオファイルを時間領域の音圧変化グラフ、及びスペクトログラムを用いて調べる。
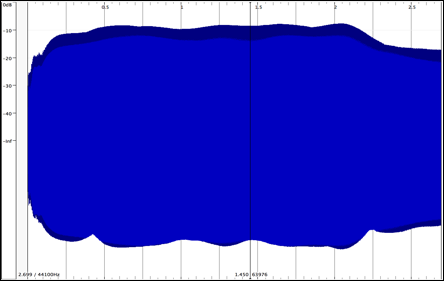
図9, グラスハーモニカのソノグラム(縦軸:周波数、横軸:時間、色濃淡:音圧)
図7から、この音声は立ち上がりから減衰するまでの間、一定の音量を出し続けているのではなく、微妙に揺らいでいる事が確認できる。この揺らぎは周波数毎に微妙に異なっている。スペクトラム表示では任意の区間の分析に限られる。そこで連続的にフーリエ変換を行う事が可能であるSonic
Vusialiserを用いてそれぞれの周波数毎の音圧変化を調査したところ、最も低い469Hzの音は耳で分かるほどの音圧の増減を行っており、その倍音である937Hzの音はゆったりとした変化を持っていた。また、2000Hz以上の音に関しては非常に早い速度で音圧が上下していた。(付録 リアルタイムFFTビデオ)
このことから、単純に加算合成すればこの音が出来るという訳ではない事が分かる。
第三章 Max/MSPを用いた合成
実際にMax/MSPを用いて合成を行う。Max/MSPはCyclyingÕ74社が販売している音響プログラミング言語である。本研究ではこのソフトウェアを用いて合成を行い、さらにその音をAbleton社製のLive 9にてリバーブエフェクトをかけることで実際に演奏されているような環境をシミュレートする。
第一節 クロスシンセシス
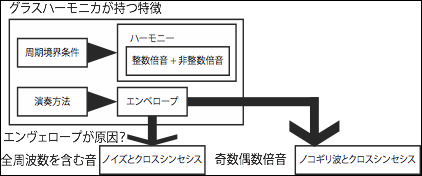
図10, クロスシンセシスの実験フローチャート
まず始めに、グラスハーモニカの音の良さはそのエンベロープ情報がもたらすものである、という仮定の検証を行うために、グラスハーモニカ音の周波数毎のエンベロープ情報を検証用の音に合成することでその特徴を付加した音を作成する。
ホワイトノイズは全周波数の音を含み、ほぼ同じ音圧を出していることから、この信号とクロスシンセシスを行うことで、元の音が再現されるはずである。
グラスハーモニカのスペクトラムをフィルターとして用いる事で、キャリア音に対してグラスハーモニカの音の特徴を受け継ぐ。二つのオーディオ信号の畳み込みは一つのスペクトルをもう一つのスペクトルによってフィルタリングする事に等しい。ただ単純に2つの音声信号を乗算するとそれは振幅変調(AM)リングモジュレーション(RM)となり、それはスペクトルを畳み込む事に等しい。スペクトルの畳み込みとは、入力aの離散周波数スペクトルの各点bのスペクトルの全ての点と畳み込むという音を意味している。
ホワイトノイズ(図11)をクロスシンセシスした。(図12)実際にクロス合成を行った音にはホワイトノイズを確かに感じられるが、グラスハーモニカの音を感じる事ができた。ホワイトノイズは全周波数の音を含むので、ノイズに感じてしまう。そこで、奇数および偶数倍の倍音をもつノコギリ波とも合成をした。(図13)このとき、グラスハーモニカのもつ基本周波数と同じ周波数でノコギリ波を発生させた。ノコギリ波は正弦波を合成することで近似する式を得る事が出来る。ノコギリ波に収束するフーリエ級数は以下のように表す事ができる。
![]() ・・・①
・・・①
この①式(スペクトラムは図15)とグラスハーモニカの音を合成したところ、図16のようなグラフになった。もともとのグラスハープのスペクトラムと比較すると、特に高域の成分が無くなっている事が分かる。結果的にフォルマントの高いピーク部分を抜き出した形になった。
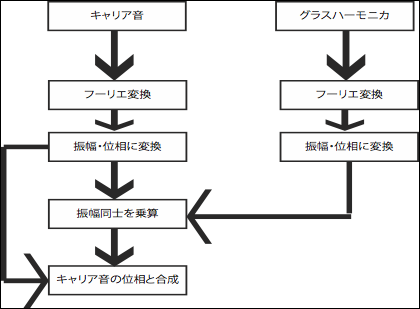
図11, クロスシンセシス手順
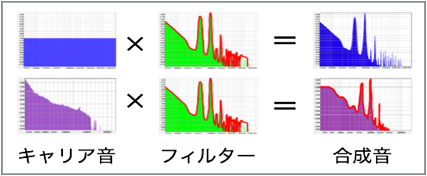
図12, クロスシンセシスイメージ図
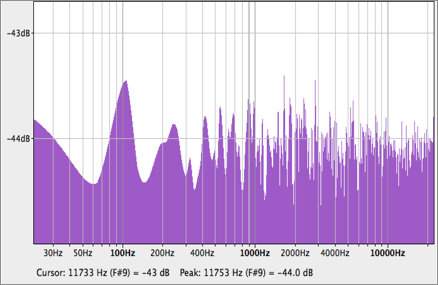
図13, ホワイトノイズのスペクトラム
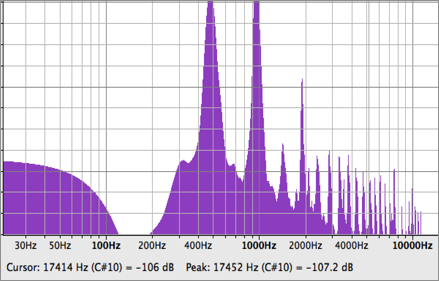
図14, グラスハープフィルタリングをされたホワイトノイズ
のスペクトラム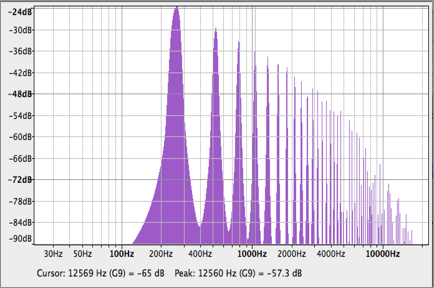
図15, ノコギリ波のスペクトラム
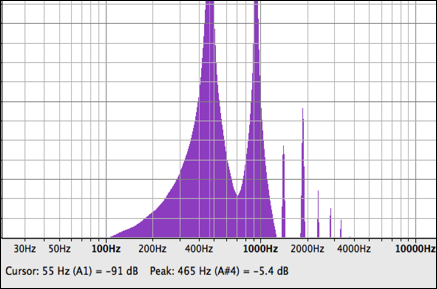
図16, グラスハープフィルタリングをされたノコギリ波のスペクトラム
第二節 加算合成
倍音が良い音の要素の一つであることは広く知られている。ではこのグラスハーモニカの倍音が美しさを生み出すという仮定で音を合成した。このとき、各周波数のサイン波のエンベロープはほぼ等しい状態にした。これは倍音のみが影響を与えるのか否かを検証するためである。
以下にその合成された音のスペクトラムを表示する。(図17)一見高周波成分の音が失われているように見えるが、これは対数グラフで表した都合上、高周波部分のグラフ幅が極端に狭くなったため、見えなくなっているだけである。実際には音を合成してある。
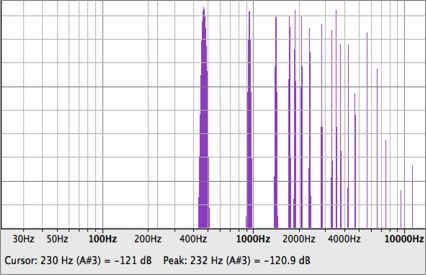
図17, 加算合成後のスペクトラム
この音を聴くと、パイプオルガンの音に近い事が分かる。もともと、グラスハープは「天使のオルガン」と呼ばれていたこともある歴史がある。倍音関係だけに注目するとそのパイプオルガンの音に近くになるのも頷ける。パイプオルガンのスペクトラムは整数倍音が綺麗に発生する音であるという事は多くの研究によって既に明らかになっていることである。
第三節 時変加算合成
エンベロープのみ、もしくは倍音のみでは自分の求めている音とは異なる事を確認した。つまり、この二つの要素を組み合わせなければ自分が求めている音が出来ないという事である。その結果から合成した音のスペクトルが以下である。(図19)
実際に音を聴いてみるとグラスハーモニカが持つ特徴に近くなっていることを確認できた。
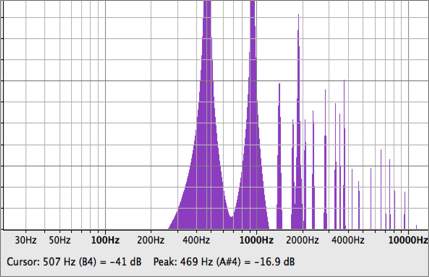
図19, 時変加算合成後のスペクトラム
第四章 結論
グラスハーモニカに含まれる音は、その周波数一つ一つのエンベロープに大きな特徴がある事が確認できた。また、倍音の構成が音に与える影響もやはり大きい物であった。それ以外の微細な変化は聞き取れなかった事からさほど重要ではないのかと思われる。実際にこの音を作成する過程で、大きく変化を起こしたのはエンベロープの変化であった。時間的な音量の変化を各周波数毎に作成する事で、非常に似た音から決定的に異なる音まで様々な変化を見せていた。指で演奏していることでこの揺らぎが出ているということが考えられることから、奏法と楽器の特徴が生み出す非常に優れた発音楽器であるという事が言える。この点に注目し、モデルを作成することができればより素晴らしい音が出来ると考えられる。
将来的にこの結果を応用し、このモデルを一般化する事で、グラスハープ、グラスハーモニカ以外の音、鈴や梵鐘などの似た形状の楽器のモデルを作成していく事を将来的な視野に入れたい。
謝辞
長年ご指導をして頂き、時には相談にも乗って頂いた岩竹徹教授に深く感謝を致します。また、好きな事を学べ、と今まで自由に活動をさせてくれた家族、父、母、弟に感謝を致します。
付録
Max/MSPパッチ図
Max/MSPパッチは付属CDに内包
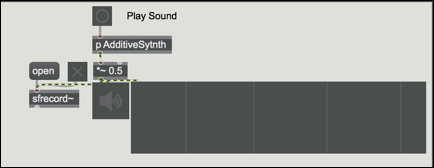
図20, インターフェース
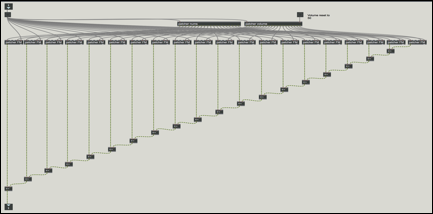
図21, 加算合成部
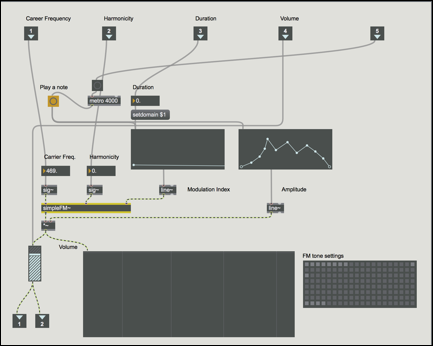
図22, FM合成部
付録オーディオファイル
別途CD参照
(注)元となったグラスハーモニカの音、およびグラスハープの音に関しては著作権の関係でCDに入れる事を控える。
収録内容(ファイル名)
1. 加算合成のみ(Additive_synthesis_only)
2. 加算合成、音量の全体変化(Additive_volumebalance_only)
3. 時変加算合成(Glass_Harmonica)
4. 時変加算合成、リバーブエフェクト付き(Glass_Harmonica_Reverb, Glass_Harmonica_Reverb2)
引用文献
1. 冨田晃,グラスハープとグラスハーモニカの概略史,弘前大学教育学部紀要. 103(2010), p73-77
2. Koichi Uchida, Kenshi Kishi,
Vubrational analysis of glass harp and its tone control , The Acoustical Society of Japan,Acoust.
Sci. & Tech. 28.6(2007)
3. 独立行政法人産業技術総合研究所, 聴覚の等感曲線の国際規格ISO6が全面的に改正に, URL: http://www.aist.go.jp/aist_j/press_release/pr2003/pr20031022/pr20031022.html
参考文献
1. Curtis Roads,青柳龍也,小坂直敏,平田圭二,堀内靖雄, 『コンピュータ音楽 歴史・テクノロジー・アート』, 電機大出版局(2001年)
2. 水本哲弥,フーリエ級数・変換/ラプラス変換,株式会社 オーム社(平成22年)
3. Romain Michon, Julius O. Smith, FAUST-STK: A SET OF LINEAR AND NONLINEAR PHYSICAL MODELS FOR THE FAUST
PROGRAMMING LANGUAGE, Proc. Of the 14th Int. Conference on Digital Audio
Effects (DAFx-11), Paris, France, September 19-23, 2011
4. 大橋力,『音と文明』,岩波書店(2003年)
5. 中村明一,『倍音』,株式会社 春秋社(2010年)
参照URL
a) Interesthingz.com, Robert Tiso Is A Spedial Kind Of Performer: He Plays A Very Unsusual Instrument, URL http://interesthingz.com/robert-tiso-special-kind-performer-plays-unsusual-instrument/
b)
Binary
Heap, URL http://reaktorplayer.wordpress.com/2010/04/05/glass-harmonica/
c)
Sugar Plum Fairy by
Tchaikovsky - Glass Harp LIVE (HD) https://www.youtube.com/watch?v=QdoTdG_VNV4
使用ソフトウェア、音源
á
Audacity
URL: http://audacity.sourceforge.net/?lang=ja
á
Sonic
Visualiser URL: http://www.sonicvisualiser.org/
á
MEISTER MUSIC, ADAGIO Wiener Glasharmonika
Duo
á
Ableton Live 9 https://www.ableton.com/ja/live/new-in-9/
á
Max/MSP https://cycling74.com/