2015年度 森泰吉郎記念研究振興基金による研究助成
研究成果報告書
確率の認知バイアスの行動・神経的ダイナミクスの解明
所属:政策・メディア研究科
修士課程 1年
学籍番号:81524177
江部 正周 Masahiro Ebe
ebe[at]sfc.keio.ac.jp
人間は認知バイアスという「思い込み」によって確率を正しく認識できていない。本研究の題材である「モンティホール問題(The Monty Hall Dilemma)」は、はじめに示された3つのドアから正解のひとつのドアを選ぶ確率ゲームであり、直感的でない確率の問題(ジレンマ)として知られている。はじめにプレイヤーは3つのドアのうち1つを選ぶが、正解の場所を知っている司会者が、プレイヤーが選んでおらず正解でもないドアを1つ開き、選択肢を2つに絞る。最終的にドアを「変えるか/変えないか」を選べるが、直感的には変えても変えなくても正解の確率は1/2である。しかしベイズの考え方により、ドアを変えた方が正解の確率が2/3と高くなる。
本研究では、このような問題をプレイヤーにモンティホール問題を知らない状態で50試行(事前ゲーム)、一週間後にモンティホール問題の考え方を教えて50試行解いてもらった(事後ゲーム)。その結果、事前ゲームよりも事後ゲームのほうがドアを変える割合が増えたが、事前ゲームで変える選択をしていないプレイヤーのほうが、事後ゲームで正しい「変える」選択をする傾向にあることが明らかになった。これはモンティホール問題の「変えないバイアス」が強いことを裏付けるとともに、はじめに試行錯誤して正しい「変える」選択をしたひとが、事後ゲームにおいても試行錯誤することでバイアスに引き戻されてしまうことを示唆する。
また、本研究は31st International Congress of Psychology (ICP2016) に応募中である。
研究概要
はじめに
人間は認知バイアスという「思い込み」によって確率を正しく認識できていない。Tversky & Kahnemanらは確率推論における認知バイアスを体系的に明らかにしてきたが、これらの研究は質問紙調査のため、いつどのように認知バイアスに意思決定が影響されるかのダイナミックな認知メカニズムは不明なままである。
そこで本研究ではGranberg, et al.(1995)を発展させ、正しい確率と直感が一致しない確率ゲーム「モンティホール問題(The Monty Hall Dilemma)」を、コンピュータ上でモンティホール問題を知らない状態で50試行(事前ゲーム)、一週間後にモンティホール問題の考え方を教えて50試行解いてもらい(事後ゲーム)、認知バイアスが影響するタイミングとそれが克服されるメカニズムを明らかにする。さらに個人レベルでの認知バイアスの理解と行動を予測する統計モデルを構築する。本研究は確率の理解の向上やビジネスでの意思決定の場面での認知バイアスの克服への示唆を与え、現実での意思決定の改善に寄与するものである。
方法
モンティホール問題 - 正しい確率と直感が一致しない確率ゲーム -
モンティホール問題とは、Monty Hall (本名 Monte Halperin)が司会をつとめるアメリカのゲームショー番組「Let’s Make A Deal」のなかで行われたゲームである。
モンティホール問題のゲームの流れを簡単に述べる。モンティホール問題の手順(右図)に示すように、この問題は示された3つドアから正解のドアひとつを選ぶ宝当てゲームである。まずプレイヤーは3つのドアのなかから開けたいドアを選ぶ。次がモンティホール問題の重要なポイントであるが、ゲームの進行役は当たりの場所を知っており、プレイヤーが選んでいないドアで、かつハズレのドアをひとつ開ける。なおプレイヤーがはじめに選んだドアが正解の場合、ランダムにどちらかのハズレのドアを開ける。そしてプレイヤーには最終的に2枚のドアが残され、はじめに選んだドアを開けるか、もうひとつのドアを開けるかを選ぶことが許される。
直感的にはドアが2つになったのだから、どちらのドアも正解の確率は1/2であるように思えるが、実際はドアを変えると正解の確率は2/3になることが証明されている。
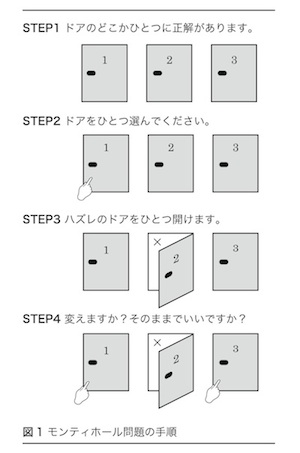
手順
実験には大学生24名が参加した。なお3名は調査2日目に参加していないため分析から除外した。
分析に含めたのは大学生 21 名(男性 8 名, 女性 13 名, 平均年齢 21 歳、標準偏差 1.34 歳)である。
事前ゲーム(教授なし)
机の上にあるラップトップコンピュータの前に座ってもらい、モンティホール問題のゲームのルールと操作方法を説明するため、以下のような教示を行った。
(1) モンティホール問題は3つのドアのなかに場所はランダムに正解がひとつ入っており、その正解を当てるゲームである。
(2) まず 1-3 の数字キーを押してはじめにドアをひとつ選択する。
(3) そのうえで先ほど指定したドアと正解のドア以外のすべてのドアが自動的に開かれる。
(4) 残った 2 つのドアで、左側を選択する場合は左の矢印キー、右を選択する場合は右の矢印キーを押す。
(5) このモンティホール問題を 10 試行 5 ブロック行い、ブロックごとに自由に休憩をとることができる。
以上のような 5 つの教示のうえ、モンティホール問題を解くに当たって注意してほしい 以下の 2 点を強調した。
(1) できるだけ多く正解を当てることが目的で、そのための戦略を考えること。
(2) その戦略を思いついたと同時にはっきりと発話すること
以上の 5 つの教示と 2 つの注意点を伝え、疑問がないことを確認して調査を開始した。
事後ゲーム(教授あり)
1週間後に、以下のようなモンティホール問題の考え方を教授し、同様にコンピュータ上で、モンティホール問題を50回解いてもらった。
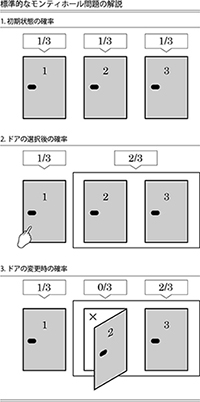
【1. 初期状態の確率】ではドアが3枚あり、当たりはランダムにおかれるためいずれのドアも正解の確率は1/3である。
【2. ドアの選択後の確率】で1番のドアをはじめに選ぶとする。ここで、はじめに選んだドアを変えない場合と変える場合とをそれぞれグループにする。すなわち、変えない場合はドアが1つで正解の確率は1/3。変える場合はドアが2つで正解の確率は2/3となる。
【3. ドアの変更時の確率】において、ここで司会者モンティは必ず外れのドアをあける(もし自分がはじめに選んだドアが正解のドアであったら外れのドアをランダムにあける)ので、変えないドアのグループの2枚のドアは1枚となるが、グループとしての確率である2/3は変化しない。
したがって、ドアを変えないと1/3の確率で正解、ドアを変えると2/3の確率で正解となり、ドアを変えることで正答率は2倍になることが示される。
結果と考察
まず教授の効果を確認するために、モンティホール問題を知らない状態で50試行解いてもらったとき(事前ゲーム)の「ドアを変える」割合と、1週間後にモンティホール問題の解き方を教授したあとに同様に50試行解いてもらったとき(事後ゲーム)の「ドアを変える」割合を比較した。
その結果、事前ゲームでは平均51%、「ドアを変える」選択をしたが、事後ゲームでは86%「ドアを変える」選択をした。これらを対応のあるt検定で検定したところ、有意に事後ゲームのほうが「ドアを変える」割合が高いことがわかった(t(20)=4.946, p<0.001)。
しかし、本実験では対照群を設けていないため、この「ドアを変える」選択の割合が時間の効果なのか教授の効果なのかは明確ではない。そこでchow検定 (Chow,G.C.,1960) と呼ばれる構造の変化、すなわち事前ゲームと事後ゲームで非連続性があるか(教授の効果があるか)を検定する統計手法を用いて検討を行った。
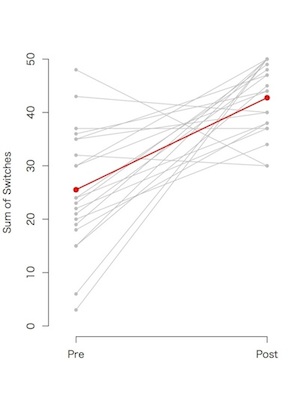
chow検定の結果、事前ゲームと事後ゲームでは有意な構造の変化があった(p<0.001)。これは教授により非連続に「ドアを変える」選択の割合が変化したことを示している。
また、事前ゲームと事後ゲームをあわせて見ると全体として「ドアを変える」選択の割合は増加しているが、事前ゲームと事後ゲームと分けて考えると、事前ゲームでは「ドアを変える」選択の割合は増加し、事後ゲームでは「ドアを変える」選択の割合は減少していることがわかる。
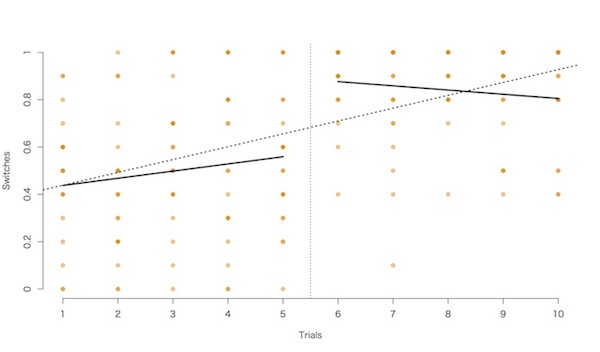
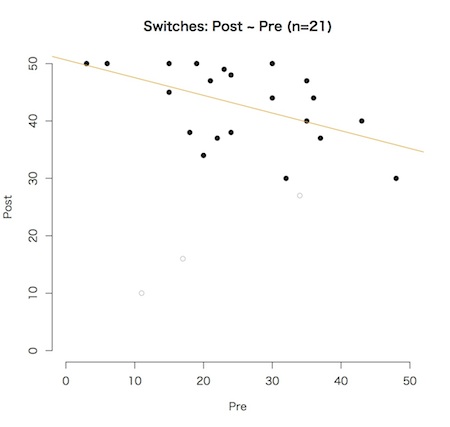
さらに個人ごとに事前ゲームの「ドアを変える」選択の割合と事後ゲームの「ドアを変える」選択の割合の散布図をとると、事前ゲームで「ドアを変える」選択の割合が高いひとほど、事後ゲームでは「ドアを変える」選択の割合が相対的に低くなっていることがわかる(r=-0.52, p<.05)。
その結果、事前ゲームよりも事後ゲームのほうがドアを変える割合が増えたが、事前ゲームで変える選択をしていない人のほうが、事後ゲームで正しい「変える」選択をする傾向にあることが明らかになった。これはモンティホール問題の「変えないバイアス」が強いことを裏付けるとともに、はじめに試行錯誤して正しい「変える」選択をしたひとが、事後ゲームにおいても試行錯誤することでバイアスに引き戻されてしまうことを示唆する。
活動報告・学会発表
本研究は31st International Congress of Psychology (ICP2016) July 24 -29, 2016 Pacifico Yokohama, Yokohama, Japan.でのポスター発表に以下の内容で応募中である。結果は3月中に発表される。学会ホームページはこちら
Title
Robustness of the non-change bias in the Monty Hall Dilemma:
Even direct instruction to change the first choice did not change the bias
Authors
Masahiro Ebe , Mutsumi Imai
Abstract
The Monty Hall Dilemma (MHD) is a probabilistic game. Most players have a non-change bias, thinking that the probability to win would be the same between the two unopened doors. However, changing the original choice actually increases the chance to win, which people find counter-intuitive. This study was conducted to examine whether teaching the logic behind the probability of the outcome by changing/non-changing the first choice would help people overcome the non-change bias. Twenty-four participants played MHD fifty times (pre-game). After a week, they received the instruction and then played the same game again (post-game). The instruction increased the rate of altering the first choice in post-game as compared to the pre-game. However, many participants eventually fell back to their original non-change bias when they experienced a few "loses," suggesting that the non-change bias was robust and just teaching the probabilistic advantage of the change- strategy would not change people's bias.
今後の展望
本研究では実験協力者の個人レベルでの統計分析を行うことができたが、今後は個人内での時系列での行動の変化を統計モデリングすることで、直感的でない確率の推論におけるダイナミズムを明らかにしていきたい。
参考文献
Granberg, Donald & Brown, Thad A. (1995). "The Monty Hall Dilemma". Personality and Social Psychology Bulletin, 21(7): 711–729.
Tversky, A., & Kahneman, D.(1980).Causal schemas in judgments under uncertainty.In M. Fishbein (Ed.), Progress in social psychology, 1, 49-72
Chow, G. C. (1960). Tests of equality between sets of coefficients in two linear regressions. Econometrica: Journal of the Econometric Society, 591-605.
ISO 690




