Part1.html

第1部基礎編

はじめに

本書の対象とする読者

本書は，慶應義塾大学湘南藤沢キャンパスにおいて行ったノリッジスキルサイエンスの授業である「数値と近似」という講義資料を基にして多少改変したものである．内容はMathematicaを使ったデータ処理のノウハウ本であるが，扱うデータはスポーツ科学にかなり偏っているといえる．スポーツ科学や人間科学を目指す学部生・大学院生向けに書いたものであるので他の分野にとってはなじみの薄いデータばかりかもしれないが，御勘弁を願いたい．

Mathematica利用の準備

システム要件

本書は下記の条件を前提として話題を提供する。
プラットフォーム Windows XP
Mathematica バージョン 5.2
ただし、Mathematicaのファイル（ノートブック）は単なるテキストファイルであるので、Windowsで作ったファイルをMacintoshに持っていっても再利用可能である（ただしグラフィックスの一部が表示されないなどの問題はある）。現在のところMathematicaが動くのは以下のプラットフォームなどである。
Windows, Mac OS, UNIX (Solaris, Linux, HP, AIX, etc)

Mathematicaの起動と終了

Mathematicaの起動は簡単である。MathematicaのインストールされているWindowsマシンであればWindowsメニューの「すべてのプログラム」にMathematicaが登録されている。

Mathematica5を選ぶ。するとMathematicaが起動する。ここで起動するのは実はフロントエンドと呼ばれるもので実際に計算するにはカーネルも起動しなければならない。フロントエンドは、ユーザーが計算式を入力したり、計算結果を表示したりする。カーネルを起動するにはカーネルメニューから「カーネルを起動\:ff0d＞Local（ローカル）」を選ぶ。

[Graphics:HTMLFiles/Part1_2.gif]

これで計算する準備が出来た

カーネルとフロントエンド

Local Kernel

カーネルとフロントエンドは、それぞれ以下の役割を担う。
カーネル：計算
フロントエンド：入出力
フロントエンドはユーザーの入力した「式」をカーネルに渡す。カーネルは受け取った式を評価して結果を「式」としてフロントエンドに返す。Mathematicaでは式のやり取りが基本となる。
このフロントエンドとカーネル、実は通信を行っている。従ってフロントエンドとカーネルが同じマシンになくてもよい。フロントエンドは自分の前にあるコンピュータであるのが普通（実はそうじゃない使い方もある）だが、カーネルは例えばCNSの速いUNIXマシンに任せるという賢い方法もある。そこでCNSのマシン上でカーネルを起動してそれに接続する方法も知っておこう。同じマシン上に存在するカーネルをローカルカーネルと呼んだりする。

Remote Kernel

新しいカーネルを設定するにはKernelメニューから「Kernel Configuration Options...」を選ぶ。すると次のようなウィンドウが現れる

[Graphics:HTMLFiles/Part1_3.gif]

ここで追加をクリックすると新しいカーネルを追加できる。

[Graphics:HTMLFiles/Part1_4.gif]

詳しくは,以下のURLを参考にするとよいだろう.
(英語ドキュメントマニュアル）
http://documents.wolfram.com/mathematica/GettingStarted/System-SpecificInformation/SpecialWaysToRunTheKernel.html

コマンドライン

Mathematicaはコマンドラインからの起動も可能である.ちょっとした計算,だけど電卓ではできないような計算をするには都合が良い。コマンドプロンプトを起動して、math.exeと入力してみよう。PATHの設定がうまく出来ているならMathematicaをコマンドラインから利用できる。描画関数のPlot[]などを実行してみるのもおもしろい。

[Graphics:HTMLFiles/Part1_5.gif]

ノートブック

ところで、この資料はMathematicaで作っている。Mathematicaのフロントエンドで用いるファイルのことを「ノートブック」と呼ぶ。ノートブックはその名の通りノートのようにして使うことが出来る。計算の過程も残せるし、書きかけのプログラムもそのまま保存できる。また計算プログラムや計算結果、グラフィックスなどを含めてすべてをHTMLに書き出すことも可能である。ノートブックファイルは、拡張子(nb)がつくが実際にはこれは単なるテキストファイルなので、テキストエディタなどで読むことが可能である。しかしながら単なるテキストファイルであるのだが，これを勝手にテキストエディタなどで修正してしまうとMathematicaで開くことができなくなる場合もあるので注意が必要である．

計算してみよう

四則演算

整数演算

実際にMathematicaを使って計算を行ってみよう。まずは基本的な整数の四則演算からはじめよう。簡単すぎるが以下を入力してみよう。

式を入力して評価するにはシフトとエンターキーを同時に押す。エンターだけでは改行となってしまう。

四則演算のルールどおりに計算が出来る。では次はどうだろうか？

0.5とはならない。整数同士の演算では式はそのまま整数として評価され実数には変換されない。ところで、掛け算をする場合、Matehmaticaでは「*」を省略することが可能である。このとき空白を入力する。例えば、2×3は次のように入力することが可能だ。

べき乗は、^（ハット）を使う

ハットを使わずに、べき乗を入力するときに「コントロール＋^」を入力すれば表示が指数らしくなる

べき乗の指数部にさらにべき乗がかかる場合には次のようになる.

これは次と同じである。

階乗っていうのもあったなあ、と思い出した人もいるかもしれない。階乗も簡単だ。エクスクラメンション(!)を使う。1×2×3は次のように表す。

1×2×3×4×5×6×7×8×9×10は

次のような計算は電卓では到底できないが，Mathematicaでないといとも簡単に計算が可能である．

分数

分数の計算も簡単だ。

ちゃんと通分してくれている。便利だ。分数を教科書のような見た目で入力したければ、BasicInputパレットを使おう。Basic Inputパレットは、「ファイル」→「パレット」→「BasicInput （基礎的入力）」で選択可能だ。

[Graphics:HTMLFiles/Part1_32.gif]

すると次のような小さなウィンドウが現れるので、この各記号をクリックして任意の数式を入力する。

[Graphics:HTMLFiles/Part1_33.gif]

練習問題

問　括弧をもちいた演算が演算子の順序に従って実行されることを確認せよ．

実数計算

実数計算はというと、どんな計算もお手の物である

Mathematicaは任意の精度の計算が可能である。実数を任意精度で表すには、関数N[]を使う。試しにπ(Pi)を小数点以下200桁まで表示してみよう

こんな具合に出力が画面幅よりも多い場合には勝手に折り返してくれる。

平方根

2の平方根を「ひとよひとよにひとみごろ…」とか、3の平方根を「ひとなみにおごれよ」などと受験勉強で丸暗記したことだろう。もう丸暗記はやめてそんなことは計算機にやらせよう。さっきのBasicInputパレットを使ってみよう。

どうしたことか2の平方根がとなってしまった。こで一つ覚えておこう。Mathematicaは厳密な数による計算を行おうとする。思い出して欲しい。2の平方根はそもそも無理数なので永遠にどこまでいっても終わることのない数である。したがって無理数である2の平方根はそのまま返される。もしも「ひとよひとよにひとみごろ…」という2の平方根を実数で知りたいという場合には、先ほど出てきた近似数を求める関数 N[ ] を用いる。

100桁まで知りたければ

少しだけ，Mathematicaの実力を感じてくれただろうか？

練習問題:

問　5の平方根を求めよ

問　-1の平方根を求めよ

変数と定数

変数

計算結果や任意の値を保持し、あとで再利用するには「変数」が使えることが望ましい。Mathematicaでは任意の変数名が使用可能である。ただし、あらかじめMathematicaが使用する変数名は別である。変数に値を代入するには、左辺と右辺をイコールでつなげる。

変数fooに1を代入してみた。では、次はどうだろう。

foo+1の結果は2になった。期待通りである。では、fooの値は？

あいかわらず1のままである。では次は

今度は，変数fooが2になった。これもおおかたの予想通りだろう。様々なプログラミング言語でも同じ結果が得られる。ここまでの手順で変数名に対して値を割り当てることが出来ることが分かっただろう。Mathematicaでは値（整数、実数、無理数、有理数…）を変数に割り当てられる以外に、様々なものを変数に割り当てられる。Mathematicaのマニュアルの原書ではこの値の代入のことをassignmentと書いている。そして訳書ではそれを割り当てと呼んでいるので、これからは極力、原書どおりに「割り当て」と呼んでいこうと思う。
次に、fooにbooを割り当てることにする。

fooがbooになってしまった。つまり何も値を割り当てられていないbooが、fooに割り当てられたわけである。ここで覚えておいて欲しいのはMathematicaは、置き換えを処理の基本としている、ということである。従ってMathematicaは、置き換えをすることが出来ればそれをまず実行する。さらに置き換えが出来るのであれば，置き換えを行う．
次に，booに値を割り当てておくことにする。

booに3.14を割り当てた後にもう一度、fooが何かを確認してみる。

先ほどはfooが1だった。次にfooにはbooが代入された。そして今、booには3.14が代入された。するとfooの値が3.14になった。先ほども述べたようにMathematicaは置き換えが可能な限り置き換えを行う。さて，間違った値を変数に割り当ててしまうことはよくあることだが、変数に値を割り当てた後で、その値をクリアしたい場合には、Clear[]という関数を使う

Global`foo

？変数名
と入力すると、その変数がどのような位置づけにあるかを表示してくれる。今、このfooはGrobal`fooとして出力されている。これはGrobalとよばれるコンテキスト(Context)のなかで用いることができる、fooと呼ばれる変数が存在する、ということを示している。コンテキストとは何か？については今後少しずつ説明していくことにする。変数そのものを消し去ってしまうには、Remove[]を使う

あらかじめ,Mathematicaが予約しているものは,変数として使うことはできないと述べたが,具体的に何が使えないのかは以下のようにすればわかる.ちょっと出力が長大なのだが気にしないでシフト＋リターンを入力してみよう

長すぎる出力なので短く、間をはしょって出力してみよう。

記号%は、「一つ前の結果」だと思って欲しい。つまりひとつ前の結果を「短く出力」するのが、関数Short[]の役割である。関数については後ほど詳しく説明を行う。

表示の抑制

ここでひとつ覚えておこう。変数に値を割り当てた場合に、割り当てた値が、Out[]= のあとに表示された。値の割り当てとともに、結果の表示、の２つの作業が行われたことを意味する。特に結果表示を必要としないときには、セミコロンを使うことで結果表示を抑制できる。

最後にセミコロンをつけないと上のように結果出力がなされる。

セミコロンをつけると結果の表示が抑制される。ただし値は割り当てられている。

計算結果や結果で返される式が長大な行数にわたる際に，セミコロンを使うことで表示をしないことができるので覚えておこう．実際うっかりして，式が長大であったり計算結果が間違っているために長い式が返される際には，その表示に時間がかかってしまうことがある．特に必要がない場合には，あるいは慣れてしまっていれば表示の抑制を行おう．

定数

変数があれば普通は定数もあるだろうと予想がつくのではないだろうか？予想通り、Mathematicaは予約済みの定数を持っている。例えば、

これは円周率パイの定数での表現である。厳密な意味をもつPiなので三角関数を適用すると

と高校の教科書どおりに答えが返ってくる。ほかにも定数がある。例えば、角度を度数からラジアンに変換するときのDegreeがそれにあたる。

このほかには,GoldenRatio, EulerGammaなどいくつかが用意されている

シンボル計算

Mathematicaはシンボル計算が得意である。Mathematicaが数式処理ソフトと呼ばれる所以である。シンボル計算って何？と思う人には、「記号での計算」とでも思っていただこう。筆者もその厳密な意味を説明せよといわれても少々困る．ここでは、中学校のときにならった計算をMathematicaを使っておさらいしよう。

シンボル同士の四則演算

簡単な整数や分数の四則演算はすでに行ったが，ここではシンボルでの四則演算を行ってみよう．結果の出力様式に注意されたい．

a * bの結果は，abと続けて表示されているが，実際には間には空白（半角スペース）がある．すなわち半角スペースは乗算を示す．

分母分子が通分できる場合には，おおむね通分した結果が返される．

さて，それではあらかじめaとbに値が割り当てられている場合には,どうなるだろうか?

シンボルにあらかじめ値が割り当てられている場合には、「置き換え」が行なわれるためにこのように数値での答えが返ってくる．さらMathematicaは置き換えが可能なかぎり置き換えを行ってくれる．

数式の展開

数式を展開するのには、Expand[]を使う。中学校、高校のときに一生懸命覚えた公式など、もはや不要だ。まずは割り当てられてしまったaとbを一度クリアしておく。

どんなに複雑でも展開してしまう。

因数分解

式の展開とは逆に、展開した数式を因数にまとめる因数分解にはFactor[]を使う。今行った計算結果を、因数分解してみよう。

展開する前の形になっていることに気が付くだろう。まれに公式どおりに因数分解できないことがある。そんなときには、最も簡単な形にしてくれる、Simplify[]という関数を使おう。

式全体にかかる因数をくくりだしたいときには，FactorTerms[ ]を用いる．

多項式の係数を取り出したいという要求もあるだろう．そのときには，Coefficitn[]やCoefficientList[]を使う．どの変数に対する係数を求めるかは指定しないといけない．指定した項の係数を求めるには，Coeffient[]を用いる．
以下の例は，x^3の項の係数を取り出す関数，Coefficient[ ] である．

多項式の項を全て求めるには，CoeffientList[ ]を用いる．次式のxに関する係数を求めるには次のようにする．返ってくる答えは，xの0次の項，1次の項，2次の項，…という並びである．

${30, 85 y^3, 0, 35 y^2, 85 + (5 y)/17}$

練習問題

問題　以下の数式を展開せよ
(2 x^3 + 3 x^2 + x -9) ( -x^2 + 3 x +2)

問題　以下の数式を因数分解せよ
-16+10 x+9 +25 +3 +9

問題：因数分解できないような式にFactor[]を作用させるとどうなるだろうか？
すなわち理論的に因数分解が出来ないことがわかっている式を入れて確認してみればよい．

代数方程式を解く

一次方程式を解く

シンボル計算，すなわち数式処理としてすぐに思いつくのは代数方程式を解くという作業であろう。Mathematicaで代数的に方程式を解くには、Solve[]を使う。まずは簡単な1次方程式で試してみよう。

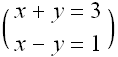
({{x + y = 3}, {x - y = 1}})

x=2, y=1という解が求まった。次は二次方程式に挑戦してみよう。中学校のときに丸暗記しただろう二次方程式の解の公式を覚えているだろうか？二次方程式の一般形、a +b x + c =0, を満たす解を求める公式のことである。

$Solve[{a x^2 + b x + c == 0}, {x}]$

${{x→ (-b - (b^2 - 4 a c)^(1/2))/(2 a)}, {x→ (-b + (b^2 - 4 a c)^(1/2))/(2 a)}}$

簡単に解が求められた．ところで，気がついたかもしれないが、
x+y==3
というふうに方程式を解く際に記述する式の左辺と右辺を結ぶのは、=ではなく==（イコールイコール）である。いったん入力してしまうと、==（イコールイコール）が、＝（イコール）に表示されてしまうので要注意である。

練習問題

問：5次方程式は一般解がないことが知られている。これをMathematicaで確かめよ。

問:  人の体格を表すにはいくつかの方法があるが、その中でも代表的なものに
    (2)Body Mass Index（BMI, 体格指数）
        BMI = 体重÷（身長(m)）^2
    (2)ローレル指数
        ローレル指数＝体重(kg)/（身長(cm)^3）ｘ10^7
などがある。BMIは22（22のとき疾病率が最低になり平均余命が最大となることから）がよいとされ、ローレル指数は160を超えると肥満とされる。自分の身長と体重を基にして自分のBMIとローレル指数を計算してみよ。
計算結果は、２つの変数MyBMI, MyRohrer,としてこれに値を割り当てよ（代入せよ）

問: 鶴と亀があわせて10匹（羽？）いる。足の数を数えてみると34本ある。鶴、亀がそれぞれ何羽、何匹いるかをMathematicaで解け。鶴が片足で眠っているなんてのはなし。

問:うさぎ（西）とかめ（東）が、1000ｍ離れている。うさぎは一分間に110m歩く。かめは一分間に10ｍ歩く。うさぎとかめがお互いの方向（つまりうさぎは東に、かめは西に）に向かって歩き出すと何分後に出会うだろうか？Solveを使って解け。

次に1000ｍ離れているとき、かめが東に向かってあるきはじめ、うさぎもかめの方に向かい東に向かって歩き始めた場合、うさぎは何分後にかめに追いつくだろうか？

Mathematicaを独習する

ヘルプを積極的に利用しよう

ヘルプとチュートリアル

さて、どんどんと新しい関数が出てくるが、どんな使い方をすればよいのか，を知る方法が準備されている。そこで話を進める前に，ヘルプを参照する方法を説明しておきたい。Mathematicaではヘルプブラウザ(Help Browser) と呼ぶ。WindowsのMathematicaであればヘルプメニューから選ぶ。Shift+F1でもよい。

[Graphics:HTMLFiles/Part1_149.gif]

下のようなウィンドウが現れるので関数名やキーワードを入力すると即座に該当するものが現れる。表示される中味は実はMathematica Reference Bookの内容である。数百ページあるマニュアルの全てをヘルプブラウザーから見ることが出来る。入力欄の下にある６つのボタンのうち、Built-in Functionsがクリックされているがこの状態でMathematicaのカーネルを起動した状態で使うことが出来る全ての関数のマニュアルを検索できる。下の表示欄には関数の説明が表示されるが実はこのエリアもノートブックになっていて実際評価して関数の動きを知ることが出来る。

[Graphics:HTMLFiles/Part1_150.gif]

?　は関数の説明

様々な関数がこれから出てくるが一通りの関数の使い方に関してはヘルプブラウザーを参考にすることが最も理解が早い。しかし手っ取り早く関数の使い方が知りたい場合には関数名の前に、?（クエスチョン）をつけると関数の使い方が表示される。

ここで「詳細」と最後に表示された部分をクリックすると、その関数のヘルプがヘルプブラウザが起動されて表示される。

Options[]は関数のオプションを表示

関数のもつオプションを知るにはOptions[]を使う。たとえばPlot[]という関数のオプションを知りたい場合には次のようにする。

リスト処理

リストとは何か？

Mathematicaにおける配列処理

四則演算や変数・定数が理解できたところで次は、いきなり大きなデータを扱う方法を学ぶ。この節では、与えられたデータの平均値や標準偏差、分散を計算する過程を通してリストの扱い方を学ぶ。平均という言葉は「日経平均」とか「平均点」とか一日に一回は耳にするかもしれない。ここで統計的なデータのみかたの基本ともいえる平均に関してMatehmatica流に求めることにしよう。
Mathematicaでは、数値に限らず全てのオブジェクト（数値、文字列、シンボル、式…）を集合として扱うことが出来る。１から10までの数列を一まとまりにして扱うには次のように{}でくくる。このように{}でくくられたオブジェクトをMathematicaではリストと呼ぶ。

{}でくくるのは数値でなくてもよい。次はシンボルa,b,c,d,eを要素とするリストである。

C言語など他の言語にも同じように配列という考え方がある。しかし配列の中味は全て同じデータ型でなければならないことが多い。しかしMathematicaではそんなことを気にしなくてもよい。例えば次のようなものも可能である。

上のリストの要素は、整数1、実数3.14、文字列"Yuji OHGI"、シンボルabcを要素とするリストである。つまり，リストにするデータの中身は、その型を意識しなくてもよいと言うことである。

次に、リストは何重にでも出来る。

どのような分野でも同じことだと思われるが、スポーツ科学分野，特に筆者の専門とするスポーツ工学，スポーツバイオメカニクスでは実験データが電気信号などのアナログデータであることが多い。従ってデータを一まとまりのリストとして扱うことが多い．そこで，このリストを扱うのに便利な関数を紹介しておく。具体的な応用は本書の応用編に登場するので期待してほしい．

リスト処理関数

リストの要素

リストの要素を表すには二重括弧[[要素番号]]を用いる。要素番号（添え字）は１から始まる。０ではないことに注意しなければならない．

要素が存在しないのに評価すると怒られる。

要素番号を指定すれば当然計算も出来る

リストのリスト（2重リスト）の場合には、[[m,n]],または[[m]][[n]]と指定する。それ以上の次元のリストにおいては、[[m,n,o,....]]または、[[m]][[n]][[o]][[....]]となる。

リストに要素を付け足す

リストに要素を追加するには、先頭に追加するのか末尾に追加するのかで使う関数が異なる。先頭に追加するにはPrepend[ ]を用いる

末尾に追加するにはAppend[]だ。

ところで、今評価しているxはどうなっているかというと

もとのままである。変数にリストが割り当てられていて、そのリストに要素を追加したいときには次の2つの関数、PrependTo[], AppendTo[]を使う

PrependTo[]で追加されたリストを確認してみると

確かに更新されていることが分かる。次は後ろに要素を追加する関数、AppendTo[]である。

リストから要素を抜き出す

リストから任意の要素を抜き出すには、Take[],Drop[]を使う

先頭から3つを抜き出すことが出来た。次は残りの要素を抜き出す方法である。

Take[]とDrop[]の使い分けが理解できただろうか？リストの何番目から何番目までといって指定するには次のようにすればよい。

3番目から7番目までを抜き出すことが出来た。Take[]やDrop[]は実験データの必要なところだけを抜き出したりするときによく使う。覚えておこう。

リストを分割する

リストをサブリスト、すなわちいくつかのリストに分けるには、Partition[]を使う。

よく使うのは以上のような関数である。徐々に実際のデータを扱うときに使い方のポイントなどを覚えていけばよい。今はこんなことをする関数があるんだ、といった軽い気持ちでいればよい。こんなことをやってくれる関数があったはずだということをあとで思い出せばよいのである。

リスト同士の演算

和と差

さて次はリスト同士の演算を学ぶ。リスト同士の演算のうち、足し算については簡単である。次のような例で分かるだろう。まずは、リストに数を足してみる

ここでわかるように,リストにただの数字を一つ加えると,リストの要素それぞれに、「値」を足すことになる。引き算も同様である。

次は,リストとリスト同士の和と差である

リスト同士の足し算は、その要素ごとの足し算をして答えを返してくれる。差も同様である。

では次のような場合にはどうなるだろうか？

返ってきた結果から分かるように、リスト同士の足し算、引き算においてはリストの長さ（要素数）が同じでなければならない。

積と商

次に積と商を実行してみよう。次のようになる。まずは和と差のときと同様に、リストと数値の積の場合は次のようになる．

予想通りの結果であったことだろう。リストに「値」を掛けたり、割ったりするとリストの要素それぞれについての演算が行われる。次はリスト同士の演算である。

和と差の場合と同じように、リストとリストの演算の場合には、各リストの要素同士の積、商が求められる。長さが異なるとどうなるだろうか？

このようにリストの長さが違う場合には和差積商のいずれを求める演算でもエラーが返される。

リストを作りだす関数

Table[]

リストの演算を学ぶ上で、リスト自体を作り出す関数を知っておくと便利であろう。テストデータを作成したり、様々なところで役に立つので覚えておこう．
まずはTable[]という関数。Tableは繰り返し処理としても使うことが可能だが、ヘルプでは次のように説明されている．

実際にどうやって使うのかというと、10個の0を要素としてもつリストを作りたい場合には次のようにして使う。

1から10までの連続する整数を要素とするリストを作りたい場合には次のようにする。

あるいは、

さらには

書式を確認しておくと次のようになる。

Table[式, {iterator, 初期値,終了値,増分}]

iteratorは省略可能であり、初期値も省略可能である。終了値は必ず必要である。また増分は指定しない場合には1つづつ繰り返しのためのiteratorを増やしてくれる。1から10までの数値を0.1づつ増やして、それをリストにしたければ次のように増分を0.1にしてやる。

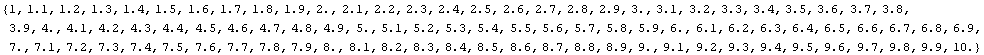
例えば、1に多少の誤差（ここでは、-0.1から0.1までの間の誤差とした）を加えた100個のデータを作りたいとするならば、乱数発生関数Random[]を使って次のようにしてリストを作ることができる

Range[ ]

次は関数Range[]である。Range[]の使い方は簡単である。連番を作るときに重宝する。

リスト処理の実例1:
Apply[ ] を用いてリストの平均を求める

平均とは

ある複数個存在するデータの傾向を知るためにもっとも多く使われるのが「平均」ではないだろうか。平均（算術平均）とは変量としての数値、,,...があるときに以下の式によって求められる。

この平均をMathematicaを使って求めてみよう。平均を求める関数を自分で作ってみてMathrmaticaのリスト処理のノウハウを学ぼう。

例題

169.5	173.5	160.5	156.0	165.0	172.5	167.3	165.9	175.1	170.2
150.1	158.0	161.0	176.8	182.3	171.0	174.6	166.5	162.3	176.8

（*）Mathematicaでは、簡単に上のような表をつくることが可能である。表作りのためのメニューをメニューバーから探してみよう。

地道に平均を求める

まずは地道に、一歩一歩進んでみよう。平均を求めるにはまずすべてのデータを足すことが必要なので、これを行う。

$General :: spell1 : スペル間違いの可能性があります．新規シンボル\"total\"はすでにあるシンボル\"Total\"に似ています．詳細$

データ数が少なければ通常はこのように、「足し算して割り算」で事足りる。しかしデータ数が100個、1000個になるとどうだろうか？割る数もいちいちデータ数と同じ数にしなければならない。
そこでMathematica流に平均値を求めてみよう。まずはデータをリストにする。
今度は、変数heightsに、上の値をリストで与えてみよう

このリストの長さ（要素数）を求めるにはどうすればいいだろうか？これには関数Length[]を用いる。

ではリストの要素全部を足すにはどうすればよいだろうか？これにはApplyという関数を使えばよい

Apply[]という関数は何をするのかというと、?で問い合わせてみると

ちょっと難しそうな説明だ。正直，筆者もこの説明の意味が分かるのにずいぶんと長い時間がかかった。ここで詳細をクリックしてヘルプブラウザを見て欲しい。するとまさに今やろうとしていることを説明しているので分かってもらえるのではないだろうか。Applyはリストに式を適用することができる（厳密には違う）。従ってリストheightsに対して、Plusという関数を適用してリストの要素を全て足し合わせてくれる。シンボル計算で確かめるとこれが分かる。

Applyを使って求める

ここまでで行った処理をまとめると、合計をまず計算した後で、データ数で割ればよいことは明らかであろう。

と簡単に平均値が求められる。では次のリストfooの平均値はどうだろうか？

おや、分数になってしまった。これは前回説明したようにMathematicaが厳密な数を用いる計算を行うことを示している。これを5.5という実数で返して欲しい場合には、関数N[]を適用してあげればよい

ところで上の式は次のようにしてもよい

//（スラッシュ2つ）は後から関数を適用するときに使う文法である．

平均を求める関数をつくる

平均は毎度毎度使うことも予想されるので、「関数化」しておこう。Mathematicaでは任意の関数を作ることが可能だ。ただし変数名と同様、すでにMathematicaが予約している変数・関数名はつけられない。平均値を求める関数は次のようにして作ることが出来る。自分専用の平均値算出関数なので、MyMeanという名前をつけよう。

関数は、
関数名[引数_(データ型)]:=関数実体
という書式でつくる。引数を囲む括弧が、[]であること、引数の後には_（アンダーバー）が必要なこと、コロン・イコールを使うことに注意しよう。この関数を先ほどのデータを計算するのに使ってみよう

うまくいった。

リスト処理の実例2:
Map[ ] を用いてリストの分散を求める

分散とは

通常たくさんの計測値（データ）をあつめてくると、それらは平均値の周りに多く集まっている（ことが多い）。これは経験上からも明らかであろう。平均値の周りにほとんどのデータが集まる場合、広くちらばる場合、色々な場合が考えられるが、このデータの広がり具合を示すものが分散である。仮に同じ平均値をもつ集団があったとしても分散が異なると下の図のようにまったく傾向の違う集団と結論づけられる。

[Graphics:HTMLFiles/Part1_276.gif]

平均0,分散1（標準偏差1）の正規分布

[Graphics:HTMLFiles/Part1_277.gif]

平均0,分散4(標準偏差2)の正規分布

分散は、すべてのサンプルの平均からの差を自乗し、それらを足し合わせることで得られる。

δ^2 = 1/nUnderoverscript[∑, i = 1, arg3] (x_i - Overscript[x, _])^2

平均値からの差を求めていることで平均値からの隔たり（ばらつき）を示していることは理解できるだろう。この際、平均値よりも大きな値と小さな値が混在する場合に二乗しなければ、もしかすると差し引き0になってしまって大きなばらつきをもっているにも関わらず、見かけ上全くばらつかない、ということも起こりうる、従って引き算した結果（残差）の二乗してその和をとっている。それでは先ほどの身長データの分散を求めてみよう。

地道に求めてみる

まずは、平均から各データを引き算する。平均値は先ほど関数を使うと求められるからそれを一度変数に割り当てておけばよい。

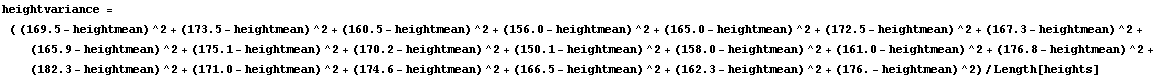
Map[]を使ってMathematica流に

平均を求めた場合と同じことが言えるのだが、データが20個だからまだ許せる。これが1000個、10000個になるとやっぱりこんなことはやってられない。これも便利にMathematica流に計算する方法を考えよう。上の計算をじっくりと眺めてみて欲しい。やっていることを順に整理すると
（１）リストのそれぞれの要素から、ある数（平均）を引いてから
（２）二乗する
（３）二乗したものを足す
（４）要素数で割る

ここではまず、最初の2工程の処理を行う方法を書き下す。
（１）リストのそれぞれの要素から、ある数（平均）を引いてから
（２）二乗する
この過程をプログラムにするには、関数Map[]を用いる。

次の工程はすでに平均のところでやったが、Apply[]を用いる。
（３）二乗したものを足す

最後の工程は、関数Length[]を使って要素数を出しておけば計算が可能である。
（４）要素数で割る

最初の工程で用いた関数、Map[]はMathematicaならではの関数であり、リスト処理には欠かせない非常に強力な関数である。使い方は以下のようにして用いる。

Map[式[#]&,リスト]

使い方はちょっと難しいかもしれない。上の説明では、式[#]&, となっている。Mapはリストの要素一つ一つに対して、式を適用する。「リストの要素それぞれ」をここでは#（シャープ）で表現している。そして実行するべき式の最後には&がくる。これを忘れないように。例えば次の簡単な例ではリストの要素それぞれに1を足した数を返す。

以下の例では、リストのリスト（2重リスト）に対してそれぞれのリストの最大値を返す。

この形式のMapの利用法を純関数（ピュア関数）と呼ぶ。今後何度も何度も出てくるので、少しづつ覚えていって欲しい。リストの要素それぞれに対して同じ操作を必要とするときなどには、常に用いるだろう。つまり、他の言語ではfor文や、while文によって行う繰り返し処理をMapを使って実現できる。「リストの要素それぞれ」に対して何かの操作を必要とする際にはたいていの場合使える。

分散を求める関数をつくる

それでは、平均と同じように分散を求める関数を作ってみよう。上で行った操作を関数化すればよいのである。

関数化されたMayVarianceを使うと

うまくいった。なんとも便利ではないか。

練習問題

問：x = {1,2,3,4,5}として，Map[ ] を用いてリストxの要素をPrint[ ]で表示せよ．

問：x = {1,2,3,4,5,6,7,8,9,10}として，xの各要素の三乗をMapを用いて計算せよ．（単純には，x^3　で計算できる．）

リスト処理の実例3:
リストの平均値・標準偏差から標準偏差を求める

標準偏差とは

になっているので、ピンとこない
分散の正の平方根のことを標準偏差(Standard Deviation : SD)とよぶ。平方根であるので次元は元データと等しくなるので、どの程度データの広がりがあるのかをつかむにはむしろ標準偏差のほうがわかりやすいときもある。正の平方根であるから、

標準偏差を求める関数をつくる

標準偏差も関数化しておこう

練習問題

問：任意の長さのリストの先頭と末尾を取り除く関数MyExtractをつくれ
例：MyExtract[{1,2,3,4,5}] -> {2,3,4}
このノートブック最初の方をよく読むように

問：任意の長さのリストを与えると、各々の要素の自乗を全て足し合わせる関数、SumSquare[]を作れ。すなわち、SumSquare[{1,2,3}] -> 14という結果が返ってくる関数を作る。最終的な結果を得るために、副関数を作っても構わない。

問：リストはベクトルとして用いてよいことは既に述べた。では、{x,y}={1,2}を2次元ベクトル、すなわちxy平面状の座標と考えると、原点からの距離Dはどのような関数を作れば求まるだろうか？Distance2[]という関数でこれを実現せよ。

次に、{x,y,z}={1,2,3}を3次元ベクトルすなわち、3次元空間上にある点の座標だと考えた場合には、原点からの距離はどのようにして求まるだろうか?Distance3[]として、これを実現せよ。

関数

毎回同じ計算をする場合には関数をつくろう

前節のリスト処理において平均値、分散、標準偏差といった「記述統計量」を求めることが頻繁にある、ということからこれらの統計量を求める「関数」を作成した。同様に、各自が今後なんらかのデータ分析を行う際には、対象とするデータは異なっても同じ計算処理を行うことが多い。従って、毎回定例作業として行うようなことは関数化しておくほうが便利である。小さな関数を組み合わせることで、さらに別の関数を作り出すことも可能になる。そこで本章は関数を作る方法を詳しく学ぶ。

関数の基本形

すでに何度か関数を作る方法は述べてきたので復習になるが、Mathematicaにおいて関数は、

関数名[仮引数_(データ型)]:=関数実体

という書式でつくる。仮引数（関数が計算において必要とするデータ）を囲む括弧が、[　]であること、仮引数の後には_（アンダーバー）が必要なこと、:=（コロン・イコール）を使うことに注意しよう。仮引数とは、関数に与えるデータに対して「仮」につけている名前であって実際にはこの仮引数のところに本来計算に必要とされるデータ、これを実引数と呼ぶ、が入力されることになる。

a+1

変数aに1を足してその答えを返す関数PlusOne[]を作ってみよう。これは簡単だろう。

この場合,整数でも実数でも答えは返されるが返された値が異なることに注意してほしい

a+b

2つの変数を足した結果を返す関数、MyPlus[]を作ろう

もしも関数に与える引数が複数ある場合には、上のようにカンマ区切りで変数を並べてやる

Max2

2つの数のうち大きいほうを返す関数、Max2[]を作ろう

関数 If[]

ここでIf[]という関数が出てきた。If[]は制御構造のうち条件式の値によって次に処理する命令を決めるときに使われる。つまり

If[条件式,真の場合の処理,偽の場合の処理]

である。Max2の場合には「もしもaがb以上ならばaを返し、そうでないならばbを返す」という風に読む。

練習問題

問：3つの数のうち最も大きい数を返す関数Max3[]をつくれ

問題：4つの数のうち最も大きい数を返す関数Max4[]をつくれ

問題：3つの数を引数とし、そのなかで最も大きい数と2番目に大きい数を足した答えを返す関数、MaxSum[]をつくれ

$MaxSum[a_, b_, c_] := Apply[Plus, {a, b, c}] - Min[{a, b, c}]$

関数定義あれこれ

引数のパターン

さて先ほど出てきた関数、PlusOne[]を少しだけ変形してみよう。その前にすでに定義されているPlusOneの定義を消し去っておこう。

Global`PlusOne

PlusOne[a_]:=a+1

Global`PlusOne

関数の定義、というよりはPlusOneに割り当てられている規則が消えてなくなった。新しい定義を与えてみる

これはさっきと一緒だ

今度はどうだろうか。計算したはずが、PlusOne[1.]というものが返ってきた。この場合、関数PlusOneの引数aのパターンは整数、という約束を関数定義の際に行ったため、整数ではない実数が与えられたときに評価されずにそのまま戻ってきた、ということである。Mathematicaは、関数の定義の際に与えられる引数のパターンを見分けてそれに応じた処理を行うことが出来る。また関数定義の際に与えられた引数パターンと異なるデータが関数実行の際に与えられると、関数は何も評価せずにそのまま返す。特にこれは忘れやすいことなので気をつけておこう。

関数の多重定義

関数はその引数パターンによって使い分けることが出来ると書いたが、これを利用すると便利なことが見えてくる。これを説明するために簡単な関数を定義してみる。さっき作ったばかりのMax2,Max3,Max4を使ってみよう

Global`MyMax

MyMax[a_,b_]:=Max2[a,b]

MyMax[a_,b_,c_]:=Max3[a,b,c]

MyMax[a_,b_,c_,d_]:=Max4[a,b,c,d]

こうすると、引数が2つのときにはMax2を、引数が3つのときにはMax3を、引数が4つのときにはMax4を使うのだろうな、と想像できるのではないだろうか？

ここまでは順調。では次はどうだろう

入力した式がそのまま返された。つまり5つの引数のパターンにあった関数定義がなかったのでそのままの形で返されたのである。このようにMathematicaでは引数のパターンを変えることで関数に多重定義を与えることが出来る。

練習問題

問：次の関数が実行されるとどのような結果が得られるか、予想したうえで実行せよ

$PrintValue[a_String] := Print["Input value \"", a, "\" is string."]$

$Input value \"Hello\" is string.$

Print[]は,カッコ内を出力する関数である。

割り当てについて再考

=(イコール)と、:=(コロン、イコール)

関数が出てきたところで一つMathematicaがもつ面白い機能を知って欲しい。割り当てに関してである。変数を作るには、左辺にシンボル（変数）、右辺に値を準備すると述べたが、そのとき左辺と右辺をつないだのは、=（イコール）であった。しかし関数の定義では、前節でみたように、:=（コロン、イコール）を使っている。この違いはなんであろうか？
実は、:=(コロンイコール)は、Delayed Evaluation　（遅延評価）と呼ばれる操作である。Mathematicaの関数では、SetDelayedと呼ばれている。「あとで、評価するよ」ということである。文章で書くと説明がしにくいので、具体的に違いを見てみよう。

ここで何も値が返ってこなかったことに注意してほしい!　つまり今評価したのではなく後で評価されるわけである。

bは、先ほどと同じく2である。

cは、問い合わせてみて初めて2という答えが返ってきた。次にaを2に変更してみる

bは2のままである。ところがcはというと

これで違いが分かっただろうか?　=の場合には、評価をした時点での変数の値を左辺に割り当てる。これに対して、:=は評価することなく式の形だけを保持し、その式が評価されるときになってはじめて値を代入して計算を行う。つまり前節のなかで述べた関数の定義は全て、DelayedEvaluationである。式がいつ評価されるのか、というかなり重要なことがこの=と、:=で制御されている。

Module[ ] による関数定義

平均値、分散、標準偏差をまとめて計算する

関数の中で計算結果を再利用したり、複数行の計算を行うにはModuleやBlockを用いると便利である。前節では平均値、分散、標準偏差を計算する関数をそれぞれつくった。これを一つ一つ計算するのではなく、まとめて３つの計算結果を返す関数、MySimpleStat[]をつくろう。作った関数をここにコピーしてきた。

これら３つの計算を一つの関数内で行おうとすると以下のようになる．

$MySimpleStat[data_] := Module[{average, variance, sd}, average = MyMean[data] ; variance = MyVariance[data] ; sd = MyStandardDeviation[data] ; Return[{average, variance, sd}] ]$

$General :: spell1 : スペル間違いの可能性があります．新規シンボル\"variance\"はすでにあるシンボル\"Variance\"に似ています．詳細$

身長データもコピーしてきた

計算結果が3つ、リストになって返ってきた。

Moduleの使い方

上の例ではModule[]というものが関数定義として新たに出てきた。今日の内容の山場である。Module[]を使えるようになればどんな関数でも作れるようになる。

Module[{arg1,arg2,arg3,....},
ここに一連の処理を書く
]

arg1,arg2,arg3は、Module内で用意した変数である。局所変数（ローカル変数）であるといえる。もしもModuleの外で同じ名前の変数があったとしても、Moduleは変数名の重複を無効にしてくれる。変数のスコープという問題である。次の例で見てみよう

Module内のiと外のiは異なるものである。正確にはModule内のiの値が局所的なのではなく、Module内のiそのものが局所的に作られている。
もっとも簡単な関数として最初に取り上げた、PlusOne[]もModule[]を使って書くことが出来る。

$PlusOne[a_] := Module[{}, Return[a + 1]]$

Moduleが返す値

ここでひとつ気をつけなければならないことがある.上の例では結果である平均値、分散、標準偏差を「リスト」にしてReturn[]で返してきた。
ひとつひとつの計算結果,すなわち「平均値」、「分散」、「標準偏差」を毎回、Return[]を使って返すことはできない。一度Return[]を使うと、Return[]の括弧内に実引数として入れられた値をユーザーに返したあとで、関数から(Moduleから）抜け出してしまう。C言語のreturn文と同じである。従って、計算結果が複数個ある際には、結果を一まとめのリストにして返す必要がある。
またModule内のどこかで、Return[]を用いてしまうと、それ以降の処理は行われない。まさにReturnする、すなわち呼び出した環境へ戻る、わけである。

練習問題

問:三角形の三辺 a 、b 、c が分かっているとき、その三角形の面積Sはヘロンの公式によって求めることが出来る。
ヘロンの公式　S =
ただし、sは、三角形の周の長さの半分
三辺の値を引数として三角形の面積を作る関数を作れ。その際、sはModule内で用意しておき、与えられた３辺の長さから計算で求めて公式で用いることにせよ。

問：偏差値とは次の式で表される。
偏差値=+50
次の得点リストを与えると、各人の偏差値を計算結果のリストとして返す関数、Hensachi[]をModuleを使って作れ

問 : 三角関数を使って次の計算結果を返す関数をつくれ。XY平面上の原点(0,0)を中心とした任意の大きさの円を描くことにする.
半径(m)と角度(度)を入力すると、X軸、Y軸のそれぞれにおろした垂線の長さ(x,y)を返す関数を作れ。度数とラジアンの変換が必要なことに注意せよ。

再帰関数

階乗計算を再帰関数で

関数の多重定義が可能であるということと、Moduleを使うとローカル変数を使うことが出来ることをあわせると再帰関数を作ることが出来る。再帰関数とは、関数の定義の中にその関数自体が現れるようなものをさす。初めて人にはまるでピンと来ないと思われるので，次の例で確認しよう。

4! = 1× 2× 3 × 4
4の階乗は，1かける2かける3かける4．なのだが，4の階乗を計算するには次のようにも考えられる。4の階乗(Factorial Number)を求めようとすると、まず3の階乗を求めておいてそれに4を掛ければよい。3の階乗は2の階乗に3をかければ…。ならばこれを関数で書いてみると、nの階乗を求める関数を、MyFactorial[n]であらわせば、MyFactorial[n-1]にnを掛ければよいのだから

やってみよう

エラーが出てしまった、Recursion depth of 256....となっている。反復計算の深さが256を越えてしまっている。上のままだと、2の階乗を求めるときは…、1の階乗を求めるには、0の階乗を求めて、0の階乗を求めるには−1の計算に関しても求めなければ、とどんどん深入りしてしまって実はきりがない。1からNまでの掛け算をするわけであるので、最後は1のときがわかればいいのであるから、

今度はうまくいった。つまり、MyFactorial[]という関数はこういう定義なのだ。まず,MyFactorial[n]の場合には

次に,MyFactorial[1]の場合には

関数をその引数のパタ-ンによって多重定義していることがわかるだろう.

ハノイの塔

ハノイの塔という話を知っているだろうか？ハノイの塔は１８８３年にフランスのパズル研究家Ｅ．リュカが考えたゲームである。リュカが考えた作り話は次のようなものである。

「インドのベナレスにある大寺院に、ダイヤモンドの針が３本立った板があり、神はその一本に６４枚の純金の円盤をはめた。昼夜の別なく、バラモン僧たちはそこにやってきて、それを別の針に移し替える作業に専念している。そして移し替えが完了したとき、寺院もバラモン僧たちも崩壊し、この世が終わるのである。」

さて、このハノイの塔のお話をプログラミングしてみよう。
ハノイの塔は、台の上に３本の棒が固定されており、そのうちの一本に何枚かの円盤がはまっています。円盤は下へいくほど半径が大きくなっています。話しを簡単にするために、一番左の棒をＡ、真ん中の棒をＢ、一番右の棒をＣとし、最初にＡに何枚かの円盤がはまっているとしましょう。棒Ｂを利用して全ての円盤をＡからＣに移してください。ハノイの塔のルールは次の通りです。
（１）一回に一枚の円盤しか動かしてはいけない。
（２）移動の途中で円盤の大小を逆に積んではいけない。常に大きい方の円盤が下になるようにする。
（３）棒を抜いて別のところに置いてはいけない
ｎ枚の円盤をAからCの棒に移動するために何回の移動が必要になりますか。1枚の円盤の移動に仮に1秒がかかるとしたら、どのくらいの年月がかかるだろうか？

解説

n枚の円盤をAからCに移そうと考えよう。そして移動回数を計算する関数をHanoi[n]としておこう。

[Graphics:HTMLFiles/Part1_397.gif]

n-1枚の円盤が隣の棒に移動したと考えるとここに至るには、Hanoi[n-1]回の回数が必要だったはずだ。

[Graphics:HTMLFiles/Part1_398.gif]

次にAの一番下にあった円盤をCに移すのに、1回だ。つまりここまでで、Hanoi[n-1]+1

[Graphics:HTMLFiles/Part1_399.gif]

そして次にBの円盤からn-1枚の円盤がCに移動してくるには、やはりHanoi[n-1]回の回数が必要なはずだ。つまり全部移動し終わるには、
Hanoi[n-1]+1+Hanoi[n-1]
→ 2 Hanoi[n-1]+1
の回数が必要であるということだ。

[Graphics:HTMLFiles/Part1_400.gif]

関数で書くと

これではさっきの問題と同じでいつまで行っても計算に終わりがない。円盤が1枚のときを考えてみると1枚だと移動回数は当然1回なので、

計算してみよう

3枚だと7回

1年は365日、1日は24時間、1時間は3600秒なので

584942000000。
なんと5849億年もかかる。

練習問題

問：得点競技であるスポーツでは審判員の主観である得点に対して公正さを保つために、最高得点、最低得点を除いた得点を評価対象にすることが多い。以下のルールにのっとって、スキージャンプの得点計算を行う関数,JumpScore[ ]をつくれ。与えるデータは

ラージヒルか、ノーマルヒルの別　 "L" or "N", あるいは0,1などでもよい
飛距離 130(m)
5人の審判員の出した飛型点,{19.5,19,18,18,17}

以下は、http://www.tbs.co.jp/sports/saltlake/rule.htmlより抜粋
ジャンプにはラージヒル（Ｋ点＝１２０ｍ）、ノーマルヒル（Ｋ点＝９０ｍ）の個人戦と、ラージヒルの団体戦（１チーム４人）の３種目が実施されます。各種目ごとに２回のジャンプを行ない、飛型点と飛距離点を合わせた合計点で順位が決定します。飛型点は、５人の飛型審判員が一人２０点満点で採点し、最高点と最低点をカットした３人分の得点を合計します。飛距離点はＫ点までを飛んだ場合を６０点とし、それより遠いか短い場合は、ノーマルヒルでは１ｍごとに２点、ラージヒルでは１．８点が加減算されます。ラージヒルで１３０ｍを飛び、５人の飛型審判員が１９．５、１９、１８、１８、１７点と採点した場合、１９．５点と１７点を除き、残りの３つの点を合計して飛型点は５５点となります。飛距離点はＫ点を１０ｍを超えたので、６０点＋１．８点×１０で７８点。この選手の得点は、５５点＋７８点＝１３３点となります。

問：再帰的関数を用いて1からNまでの合計を計算する関数をつくれ

問：1円玉、５円玉、１０円玉、５０円玉、１００円玉、５００円玉の各々の枚数を入力すると合計金額を算出する関数を作成せよ。これが出来た人は、その金額を最小の硬貨枚数として換金した結果の各硬貨の枚数を返す関数を作成せよ。
ヒント：割り算の際の余りを求めるには、関数Mod[ ]が使える

制御構造

Mathematicaでプログラミング

関数を学ぶと色々と出来ることが広がってくる．さらに必要となる知識は，プログラミングの知識である．Mathematicaには強力なプログラミング機能も備わっているが、プログラミング言語においてはプログラムの動作を規定する上で制御構造に関して知っておかなければならない。
この制御構造には、３つの構造しかない
（１）直線型
（２）繰り返し型
（３）分岐型
である．
このうち繰り返し処理は大量データに対して何かの操作をしなければならない際に用いるし、分岐処理はデータ処理のなかで決まった条件のときだけ、ある処理を行うといった場合に必要になるので双方を知っておかなければならない．

なお，Mathematicaはプログラム言語のなかでは，命令文を逐次処理していくことからインタープリター言語であるといえる．そしてその文法はいくつもの言語のよいところを吸収しているといえる．

繰り返し処理

繰り返し処理（ループ）には、条件式を満たす場合に繰り返しを続ける、というタイプの関数For、Whileと、あらかじめ定めた繰り返し回数だけ処理を続けるタイプの関数Do、Tableがある。Tableは厳密には繰り返し処理の関数とはいえないかもしれないが、実質繰り返し処理として使うことが多い上、実際にデータ処理においては重宝するためにここで取り上げる。

For

まずは関数、For[]を紹介する。Forの使い方はC言語などのfor文と非常に似ている。

For[ 初期値, 条件式, 増分処理, 毎回の処理内容]

例えば、1から5までの数を足していき、足すごとにその結果を出力するという処理は以下のようになる。

練習問題

問：For[ ]を用いて，1から10までの整数の２乗を計算し，表示するプログラムを作れ

問：１０個の乱数を１次元リストとして作成し，このリストの１個目から１０個目までのデータをひとつひとつ加算して，加算するごとに表示出力(Print[ ] を用いる) する関数を作成せよ．

While

次は関数While[ ]である。これも他の言語と同じような使い方をする。Forで行った例をWhileで書き直すとどうなるか？試してみよう。

While[条件式, 真のときに実行する処理]

$General :: spell1 : スペル間違いの可能性があります．新規シンボル\"sum\"はすでにあるシンボル\"Sum\"に似ています．詳細$

ForとWhileの使い分けだが、一般的にはForはあらかじめ繰り返し回数が分かっている（明示的に終わる条件を決められる）ような場合、Whileは繰り返し回数が分かっていない場合、に使われることが多いようだ。すなわち終了条件にマッチするとWhile[ ] ループから抜け出す，という使い方が多い．

次は関数Do[ ]である。Doも繰り返し処理を行う関数である。条件式が真の間繰り返しを行うForやWhileと異なりあらかじめ定められた繰り返し回数だけ実行される。

Do[ 毎回の処理内容, {繰り返し回数}]
Do[毎回の処理内容, {変数, 変数初期値, 変数終了値}]

2重ループも行えることがヘルプからわかる。やってみよう。九九の計算をやってみよう．全部は大変なので3の段まで表示してみる

Table

関数Tableは、同じく繰り返し処理をする関数であるが，結果がリストになって返ってくるところが異なる。For, While, Doの3つの関数は呼び出し側に何か結果を返す、あるいは表示を行う処理を自分で書かないと計算結果を得ることは出来ない。これに対してTableは，結果をリストにして返してくれる．筆者はよくこのTableを使うことがある．

Table[毎回の処理内容（＝リストの要素となって返ってくる）, {繰り返し回数}]
Table[毎回の処理内容（＝リストの要素となって返ってくる）, {繰り返しのための変数、変数初期値、変数終了値}]

九九の計算を結果だけ返すようにTableで書いてみよう．たった1行で書けてしまう．

For, While, Do, の速さ比べ

繰り返し処理はプログラミング中に多用されるが，大きなプログラム中で占める実行時間のうち繰り返し処理にかかる時間は相当大きい．したがって，繰り返し処理を効率よく実行することが速い計算のコツでもある．そこで，For, While, Doのそれぞれの速さがどのくらいか確かめてみよう．
関数の実行時間を知るには，Timing[ ] という関数が用意されている．これを用いて事項速度を調べてみよう．

まず１０万個の整数列を用意する．

For[ ]の場合

While[ ]の場合

Do[ ] の場合

Do[ ]が一番速いことが上の結果では示されている．For/Whileでは毎回の繰り返しにおいて終了条件の判定が行われるために，速度が遅くなっていることが挙げられる．処理内容によっては，Map[ ]を使うとMathematicaでは高速な処理が実現できるが，それは問題に依存するために必ずしもMap[ ]がよいとはいえない．

分岐処理

分岐処理には他の言語同様、いくつかの分岐処理が用意されている。条件式が満たされた場合にどの処理に向かうのかを示す分岐処理はプログラム中に欠かせない。最低限のものを覚えておこう

分岐処理の基本は，やはりIf[]であろう．条件にあった場合に決められた処理を行う．

If[条件式, 真のときの処理, 偽の時の処理]

関数Ifを使って、絶対値を返す関数を作ってみると次のようになる。

IF \:ff5eELSE構文は？という声が聞こえてきそうであるが，If[ ]文の偽の際の処理に更にIf[ ]を書き連ねることで，IF \:ff5eELSE構文は実現可能である．

練習問題

問：入力した整数が偶数であれば，「偶数です」，奇数であれば「奇数です」というメッセージを出力する関数を作れ

問：2つの数値(a, b)を入力し，1つ目の数(a)よりも2つ目の数(b)が大きいかあるいは等しいときには，a+bを返し，そうでない場合には，a-bを返す関数を作れ

Switch

Switch[ ]は，式がパターンにマッチした場合にその処理を行う．最初にマッチしたパターンの処理をするので複数のパターンにマッチするような場合には注意が必要である．

Switch[式, パターン1, パターン1にマッチしたときに行う処理, パターン2, パターン2にマッチしたときの処理, ....., _, どれにもマッチしない場合の処理]

関数Switchは、式がパターンにマッチするかどうかを順に比較していき最初にパターンに一致したときの処理を行う。それ以降のパターンに一致したとしてもそれは実行されない。
3の倍数かどうか、あるいは3で割ったらあまりがいくつになるのか、によって表示を変更するプログラムは次のようになる。

例題

ThreePatterns[x_] := Switch[Mod[x, 3], 0, Print[x, " は3の倍数です"], 1, Print[x " は3で割ると1余ります"], 2, Print[x, " は3で割ると2余ります"]]

Which

Which[条件式1, 条件式1が真の場合の処理,　条件式2, 条件式2が真の場合の処理, .....条件式n, 条件式nが真の時の処理]

Whichは、条件式とそれが真のときに実行する処理の組が順に並べて使う。先頭から条件式を順に評価していき最初に真になったときの、処理を行いそれ以降の処理は行われない。全ての条件式が偽であり処理内容が見つからない場合には、WhichはNULLを返す。Mathematicaヘルプファイルからの例題を以下に示す。

[Graphics:HTMLFiles/Part1_504.gif]

0以上で，1をとるステップ関数を表現すると以下のようになる

[Graphics:HTMLFiles/Part1_507.gif]

練習問題

問：任意の三角波を，Which[ ]を用いて表現せよ．

問：任意ののこぎり波を，Which[ ]を用いて表現せよ．

ファイルの入出力

観測データや実験データをMathematicaで解析しようとすると当然ならが実験データファイルを読み込む必要が出てくる。また解析が終わればその結果を別のアプリケーションで確認したり、他の人へ渡したりする必要が出るため、データをファイルに書き出すことも当然必要になる。ここでは、ファイル入出力について紹介しておく。実際の使用法については、第2部実践編以降で何度も登場する。

ファイルからの入力

ReadListを使ったテキストデータの読み込み

ディスク上（HDDや，CD-ROM, DVDなど）に存在するテキストデータを読み込むには、ReadList[]を用いる。ReadList[ ]にはいくつものオプションがあるが簡単な例で試してみよう。例えばWindows OSにおいてMy Documents以下のあるディレクトリ内に、"data.txt"というファイルが存在していて、そのファイルの中味が次のようであるとする。

1 2 3 4 5
6 7 8 9 10

ここでは見えないが，実際のデータ区切りはタブ(\t)である。
このデータを読み込むにはまず、このファイルが存在するディレクトリに移動しなければならない。今，Mathematicaが参照している（データを読み取ることのできる）ディレクトリ（フォルダ）のことをカレントディレクトリと呼ぶ．まずはカレントディレクトリをこのファイルが存在するディレクトリに移動することが必要である。すなわち，UNIXでいえばChange Directory (cd)をするわけである。今カレントディレクトリはどこになっているかを知るには、Directory[ ]を使う。

$C:\\Program Files\\Wolfram Research\\Mathematica\\5.2$

デフォルト（初期設定）では，カレントディレクトリはMathematicaがインストールされたディレクトリになっている。そこでデータの存在するディレクトリに移動してやる。カレントディレクトリを移動するには、SetDirectory[ ]を使う。
ここでは，

$SetDirectory["C:\\home\\ohgi\\Research\\2006\\MathBook\\ImportData"]$

$C:\\home\\ohgi\\Research\\2006\\MathBook\\ImportData$

カレントディレクトリを移動することが出来た。ではカレントディレクトリにどんなファイルがあるだろうか？カレントディレクトリ上のファイル名を表示するには、FileNames[ ]を使う。

一覧で存在するファイル（ディレクトリを含む）が表示された。目的のdata.txtもある。ではdata.txtを読み込もう。

1行には5列のデータがあり、それがあらかじめ数値であるとわかっているため、上記のようにオプションで、{Number,Number,Number,Number,Number}と指示した。なんとなく使い方の概略が分かっただろうか？

ReadList[ ]の注意点

ReadList[ ]を使う際には，テキストファイルでデータがどのような配列で記録されているのかをあらかじめ知っている必要がある．
上の例では，"data.txt"は1行に5つの列をもち，そのそれぞれの列き書かれたデータは全て数値である，ということを明示している．すなわちどのようなデータがどのような書式で記録されているかを知らないと，ReadList[ ]を使うことが出来ない．
記録されているデータに空欄があったりすると，そこがエラーになるために注意が必要である．

Importを使った様々なファイルの読み込み

いくつかのファイルについては、Mathematicaで読み込む際に関数Import[ ]を用いればよい。読み込んだデータがグラフィックスの場合にはそれはグラフィックスオブジェクトとして関数Show[ ]を使って表示することが可能である。関数Import[ ]は画像だけでなく多彩なフォーマットをサポートしている。

CSVファイル

用意されたデータが、CSVファイル（Comma Separated Valuesファイル）、すなわちデータがカンマで区切られているファイルを読み込む場合には拡張子が、.csvであれば関数Import[ ]を使うことで簡単に実現できる。例えば、先ほど登場したデータファイルが次のようにカンマで区切られていて、ファイル名がdata.csvであったとすると

1,2,3,4,5
6,7,8,9,10

とすることでファイルからの入力が可能である。

エクセルファイル

元データがマイクロソフト社のエクセルファイルであれば，"XLS"の指示を指定することで読み込める可能性がある．

関数Import[ ]は、これ以外にもグラフィックス(JPEG, GIF, PNG, BMP etc)、音声(WAV,AIFF)、科学データ(GISや、医学用途のDICOMなど）、様々なデータを読み込むことが出来るが，ここでは詳しく述べないことにする。詳しくはヘルプを参照して欲しい．

Read を使ったデータの読み込み

ReadList[ ]は，データファイルの全体を読み込んでくる．ところが，全部を読み込むのではなく処理の最中に次々にデータファイルの中身にアクセスしてデータを読み込みたいこともある．そのようなときにはRead[ ]を用いる．
C言語などのプログラミング言語を学んだことがある人ならすぐに使い方はわかるであとう．
まず，ファイルへのストリームを確保する．以下の例では，"data.txt"というファイルへのストリームを，変数streamという名前でもつ．

1 2 3 4 5
6 7 8 9 10

このストリームから1つ目のデータを「数値」として読み込む

次のデータを同じく数値として読み込む.

自動的に次のデータを読み込んでいる．すなわち現在読み込もうとしているポインタは，ひとつ先まで自動的に進んでいることを意味する．
データを読まずに，とばす（スキップする）には，Skip[ ]を用いる

これで数字ひとつ分を読み飛ばしたことになる．型を指定しないとその行全てをスキップする．

確かにひとつデータを読み飛ばし，次のデータを読み込んだことが分かる．
ファイルへのストリームをクローズするには，Close[ ]を用いる．

プログラムが高度になってきてファイル内のデータを参照しながら計算を行うような際には活用してほしい．

ファイルへの出力

Save[ ] : Mathematicaデータ形式での出力

次はファイルにデータを書き出す方法を学ぶ。これにはテキストファイルで書き出す方法とバイナリファイルで書き出す場合があるが、バイナリファイルにしてしまうと後で見ても何がなんだかわからない。やはりテキストファイルにしておいた方がよい（ただし、データが巨大である場合は除く）。次にテキストデータへの書き出し方法だが、これにも2通りある。一つ目は先の読み込み方式の逆で、データをタブ区切りなど指定したフォーマットで保存する方法。もう一つは、Mathematicaのデータ形式そのままで保存する方法である。あとで再度Mathematicaでデータを利用することが分かっていれば後者の方法が便利である。Mathematica形式でデータを保存するには、Save[ ]を用いればよい。

Save["ファイル名",Mathematicaオブジェクト名1,Mathematicaオブジェクト名2,....]

例えば、次のようなリストをMathematicaデータ形式としてファイルに保存するには

$SetDirectory["C:\\home\\ohgi\\Research\\2006\\MathBook\\ExportData"]$

$C:\\home\\ohgi\\Research\\2006\\MathBook\\ExportData$

テキストエディタで確認して欲しい。確かに保存されているはずである。確認するには次のコマンドをMathematicaで入力してもよい。

foo = {{1, 2, 3, 4, 5}, {6, 7, 8, 9, 10}}

Mathematica上での式の表現方法そのままがテキストファイルに記録されていることがわかるだろう．

Export[ ]

Mathematicaのデータをテキストファイルに保存するには、ほかにもいくつかの方法がある。Export関数を使う方法もそのひとつである。
Export[ ]関数は、拡張子を指定すると、その拡張子から推測される適切なファイル形式でデータを保存してくれる。例えば、上の例では、エクセルなどの表計算ソフトで読み込める形式になれば、どこでも活用が可能であるわけだから、CSV形式などでもよい。従って拡張子をそのようにするべく指定してみる。

CSV形式

エクセル形式

TAB区切り形式

低レベル関数による方法

すべてをマニュアルで指示して保存する方法もある.それには,低レベル関数WriteString[ ]などのファイルI/O関数を用いる。その際には、お決まりのパターンがある．
（１）ファイルを開く(OpenWrite[ ]）
（２）ファイルに書き込む(WriteString[ ])
（３）ファイルを閉じる（Close[ ])
という手順をとる。改行なども自分で明示的に指示しなくてはならない。先ほどの1から10までの数値データfooを，2行5列の形式（Mathematica内では2重リスト）にして低レベル関数でファイルに書き出す方法は次のようにすればよい。

書き込まれたファイルの中身を確認してみよう

1,2,3,4,5
6,7,8,9,10

カーネルイメージのダンプ

データをファイルに保存するには違いないが、ちょっと用途の異なるファイル出力がある。カーネルを起動していて計算を行っている際、作業を中断することは当然起こりうる。その際に、作業途中経過をすべて保存しておいて次回Mathematicaを起動した際には、そこから続きの作業を行いたい場合がある。これには、関数DumpSave[ ]を用いる。

すると指定したファイルに今現在のすべての定義（つまり、変数名や変数に割り当てた値，関数の定義などを含めてカーネルの状態全て）が保存される。再度これを読み込むには、次のようにする。

バイナリファイルの入出力

バイナリファイルの入力

実際のデータ待ち

バイナリファイルへの出力

実際のデータ待ち

文字列

文字列の操作は，必ずしもデータ処理のなかで出てくるとは限らないが，オブジェクトとしての文字列は色々なところで頻繁に出てくるので知っておいたほうがよいだろう．Mathematicaでは，バージョン5.1からさらにパワーアップした．Wolframからの紹介では遺伝子配列のような大規模な文字列も相手に出来るほど関数群が洗練されたようである．

文字列操作関数

文字列操作の基本

ためしに簡単な文字列で確認してみよう．Mathematicaでは文字列も実はリストとして扱われる．

StringLength : 文字列の長さを知る

文字列の長さを知るには，関数StringLength[ ]を用いる．

ピリオド，空白を含めて19文字であることが確認できた．

StringJoin : 文字列を結合する

文字列を結合するには，StringJoin[ ]を用いる．

これと同じことは，演算子<>を用いても可能である．

StringTake : 任意の文字列を抜き出す

任意の場所の文字列を取り出すには，StringTake[ ]を用いる．これはリスト関数のTake[ ]と同じ使い方をする．

StringDrop : 任意の文字列を抜き出す

任意の位置にある文字列を取り出す場合には，StringDrop[ ]も使うことが出来る．これもリスト関数Drop[ ]と全く同じように使用することが出来る．

StringReplace : 文字列を置き換える

ある文字列を別の文字列に置き換えるときには，StringReplace[ ]を用いる．

こうした文字列操作関数のほかに，大規模な文字列の操作が出来る関数も用意されている．これらは，Mathematica 5.1から導入されているものであるのでヘルプファイルのなかの，「ハイライト：言語と中核システム」を読んでみるとよいだろう．

グラフィックス

Mathematicaにおけるグラフィックスの基本

計算結果や実験結果、あるいは研究の成果を効果的に人に見せるには、適切なグラフを選ぶ必要がある。本節では数学的な知識とは少し離れるがMathematicaを使って効果的なグラフを作成する手法を学ぶ。Mathematicaのグラフには大きく分けて、

2次元グラフ
3次元グラフ

の２つがある。またそれぞれについて、

関数形を表示するためのグラフ関数
データを表示するためのグラフ関数

が備えられている。「関数形を表示する」とは例えば、y=x+1　のグラフを表示するといった用途の場合である。「データを表示する」というのは例えば、リストで用意されたデータ{1,2,3,4,5,6,7,8,9,10}を表示するといった用途の場合である。また実際にはグラフは、グラフィックス原始関数(Graphics Primitives)を組み合わせて作られている。グラフィックス原始関数も知っておくと、用意されたグラフ関数だけでは不十分な場合に威力を発揮するので、勉強しよう。

2次元グラフ(関数形の表示)

2次元グラフの基本

まずはもっとも基本といえる関数を表示する2次元グラフを描く

[Graphics:HTMLFiles/Part1_573.gif]

y=2xを描画した。次は、y=を表示してみる

$Plot[x^2, {x, -1, 1}]$

[Graphics:HTMLFiles/Part1_577.gif]

よーくみてみると、Out[2]=-Graphics-とPlot[ ]の結果が返されてきていることに気がつくだろう。そこで、上の2つの表示を一旦ある変数へと格納しておこう

[Graphics:HTMLFiles/Part1_580.gif]

$g2 = Plot[x^2, {x, -1, 1}]$

[Graphics:HTMLFiles/Part1_583.gif]

[Graphics:HTMLFiles/Part1_586.gif]

２つのグラフを重ね合わせることが出来た。実はPlotなどのグラフ表示関数で返されてきているのは、グラフィックスオブジェクトと呼ばれ、これをShow[ ]という関数を用いることで再度描画することが出来る。

関数Plot[ ]のオプション

ここでPlot[ ]を確認しておこう

Plot[式, {x,xmin, xmax},opt___]
opt___には様々なオプションがはいる。

こんなにたくさんのオプションがある。よく使うのは、下記のようなオプションだろう

軸に名前をつける

[Graphics:HTMLFiles/Part1_591.gif]

グラフの外枠を描く

[Graphics:HTMLFiles/Part1_594.gif]

グリッドラインを描く

[Graphics:HTMLFiles/Part1_597.gif]

横軸には、{-0.5,0.5}の位置にグリッドラインをひき、縦軸のグリッドラインはAutomatic(自動)にしてみた。

グラフ自体に名前をつける

[Graphics:HTMLFiles/Part1_600.gif]

おや、AxesLabelと同じ位置に出力されてしまって重なってしまっている。少しは考えなければならない場合もあるようだ。

グラフの線を太くする（細くする）

[Graphics:HTMLFiles/Part1_603.gif]

PlotStyle→Thickness[0.05]では線の太さ(Thickness)が、グラフの横軸の幅を1として、その何倍かを指示することで線の太さを変えられる。線の太さはグラフを拡大・縮小してもグラフ全体の大きさに対する比となる。

[Graphics:HTMLFiles/Part1_606.gif]

PlotStyle→AbsoluteThickness[5]では線の太さ(Thickness)が、グラフの大きさによらず絶対的な太さで決まる。単位はピクセル(1/72 inch)である。この場合は、グラフの拡大・縮小を行っても線の太さは一定である。

線の色を変える

[Graphics:HTMLFiles/Part1_609.gif]

線の色はRGBColor[R,G,B]もしくは、Hue[ ]、GrayLevel[ ]などで指定できる。

[Graphics:HTMLFiles/Part1_612.gif]

[Graphics:HTMLFiles/Part1_615.gif]

縦横比を変える

次のグラフをよく見ると縦と横の比率が違っていることに気がつくだろう。

[Graphics:HTMLFiles/Part1_618.gif]

もしもこの縦と横の比率が1:1でなければならないようなときには次のようにすればよい

[Graphics:HTMLFiles/Part1_621.gif]

Defaut設定(初期設定)では,AspectRatio→1/GoldenRatio （つまり黄金比率）となっている。

複数関数の同時描画

複数の関数を同時に描画するには、Plot[ ]にリストで関数形を与えてやる。

[Graphics:HTMLFiles/Part1_624.gif]

どっちがどっちだか分かりにくい。そこで片方を破線にしてみよう

[Graphics:HTMLFiles/Part1_627.gif]

このようにリストで関数形を与えた後で、オプションのうち、PlotStyle→{}の中もリストで各関数形の表示形式を指定すればいくつもの関数形を同時に分かりやすく表示できる。色をつけることは既に覚えたはずだから、それを応用すれば

[Graphics:HTMLFiles/Part1_630.gif]

このように複数グラフは様々な方法で分かりやすく表示できる。

DensityPlot

デフォルトで用意されている2次元グラフには、あと２つある。その一つがDensityPlot[ ]である。DensityPlot[ ]は、横軸x, 縦軸yの変化によって、xyに直交するz軸の値が変わるような関数形の時に用いる。ある座標の濃度を示しているといえる。また3次元グラフのある面で切断した断面を見ているといっても良いだろう

[Graphics:HTMLFiles/Part1_633.gif]

PlotPoints→25は各軸を何等分にしてみせるか、というオプションである。細かくすればリアルになってくる

[Graphics:HTMLFiles/Part1_635.gif]

[Graphics:HTMLFiles/Part1_637.gif]

縦と横のメッシュの切り方を変えることもできる

ContourPlot

もう一つの2次元グラフはContourPlot[ ]である。こちらはDensityPlot[ ]に似ているが、同じ値のところを結んで値が大きければ濃度を濃くして見せるというものである。等高線図と思ってもらえばよい。

[Graphics:HTMLFiles/Part1_639.gif]

3次元グラフ(関数形の表示)

基本

関数形が3次元になった場合には、Plot3D[ ]を使うのが基本である。

Plot3D

[Graphics:HTMLFiles/Part1_641.gif]

たくさんのオプションがあることが分かるだろう．ではメッシュを細かくしてみよう．

[Graphics:HTMLFiles/Part1_646.gif]

視点を変える

描いたグラフを裏側から見たい場合や下から覗き込みたいこともあるだろう。そういうときには描画する際に視点を変えてやればよい。Inputメニューをプルダウンすると、3D ビューポイントの設定というメニューがある。これを呼び出そう。

[Graphics:HTMLFiles/Part1_648.gif]

ここで表示される3次元のグリッドをマウスでくるくると回転させることで任意の視点から見ることが出来る。視点を決めたら、Pasteをクリックしよう

[Graphics:HTMLFiles/Part1_649.gif]

カーソルのある位置に次のようなものが貼り付けられたはずだ。

これを先ほどのPlot3D[ ]のオプションとして渡してやればよい。

[Graphics:HTMLFiles/Part1_653.gif]

これは下から覗き込んだところ

リアルタイムで視点を変える

上の方法では、視点を変えるたびに再描画しなければならなかった。Windows/MacintoshのMathematicaでは、これをリアルタイムで視点変更できるパッケージ、RealTime3Dが利用できる。まず、このパッケージを読み込む

さっきと同じようにPlot3D[ ]を実行する

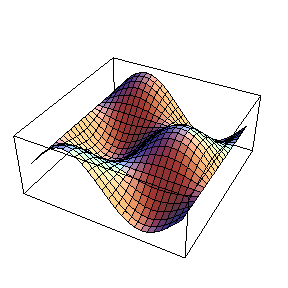
-SurfaceGraphics-

グラフをクリックしてマウスでぐりぐりと動かすと視点を変えることが出来る。こんなことが出来るのもMathematicaの強みだ。RealTime3Dをオフにするには、次のコマンドを入力する。以降の節を進めるために元のグラフィックス表示に戻したいので次のコマンドを入力してほしい。

2次元グラフ(リストデータの表示)

基本

先ほどまで2次元、3次元とグラフを描いてきたが、それは関数形として式が与えられた場合のみ可能であった。実験データや調査データなど描画したいものが数値データである場合には、Plot[ ]やPlot3D[ ]が使うことができない。その場合には、ListPlot[ ], ListPlot3D[ ]といった関数が用意されている

ListPlot

[Graphics:HTMLFiles/Part1_663.gif]

小さな点だが、リストになったデータが描画されたことが分かるだろう。リストが1次元ベクトルの場合にはこうして、リストのなかでのデータの順番が横軸(x軸）の座標となる。
データが，{x,y}にように組になっているものであれば，それぞれがx座標，y座標に割り当てられて描画される．

[Graphics:HTMLFiles/Part1_668.gif]

ListPlot[{{x1,y1},{x2,y2},{x3,y3},...},opt___]
の場合には,x軸、y軸の値が各軸の値とし採用される。

上のグラフはちょっと点が小さすぎて見にくい。点を大きくしよう。

[Graphics:HTMLFiles/Part1_671.gif]

Plot[ ]のオプションで線を太くしたように点を描画するListPlot[ ]では、点を大きくするPointSizeというオプションがある。線でつなぐには、PlotJoined->True or Falseのオプションを使う。

[Graphics:HTMLFiles/Part1_674.gif]

ListPlot[ ]のオプション

ListPlot[ ]がよく使う関数である。オプションもたくさんあるが覚えておくとよいオプションのほとんどはPlot[ ]のものとほぼ同じである。線でつなぐPlotJoined→True(False)などには違いがあるが、Plot[ ]と共通しているものが多いのでたいていは使えると思っておいてよい。

ListDensityPlot

DensityPlot[ ]に準じて、ListDensityPlot[ ]が用意されている。与えるデータは2次元リストであればよい。

$data = Table[Sin[x]/Cos[x^2 + y^2], {x, -2, 2, 0.1}, {y, -2, 2, 0.1}] ;$

[Graphics:HTMLFiles/Part1_680.gif]

ListContourPlot

ContourPlot[ ]に準じてListContourPlot[ ]が用意されている。

[Graphics:HTMLFiles/Part1_682.gif]

ListContourPlot[ ]などの関数は、GIS関連の研究をしている人ならば有用かもしれない

練習問題

問：次のデータは落下するボールの位置を計測した実験データである。初速度0で落下したボールには重力しか働かないので、理論どおりだとするとその軌跡は、y=4.9t^2の位置にあるはずである。実験データのボールの軌跡を点で描画し、理論値であるこの式の関数形を同じグラフ上で表示せよ。その際、理論値の関数は赤線で示し、実測値は多少大きめの黒丸で示せ。
data = {{t1,y1},{t2,y2},{t3,y3},.....}}の並びとなっている。

次のような出来上がりにせよ

[Graphics:HTMLFiles/Part1_684.gif]

3次元グラフ(リストデータの表示)

基本

3次元のリストプロットは、ListPlot3D[ ]を使うのが基本である。データをリストで用意しておこう。

ListPlot3D[ ]

[Graphics:HTMLFiles/Part1_688.gif]

間違いやすいのが(私も頻繁に間違うのだが…)、{{x1,y1,z1},{x2,y2,z2},....}の3次元座標でデータを渡すのではなく、ListPlot3Dに渡すのは
{{z11,z12,z13,,,z1n},{z21,z22,z23,...z2n}...{zm1,zm2,zm3...,zmn}}　のように鉛直方向の値に相当するデータを2次元配列として渡す点である。つまり高さ方向に対するグラフを描くというイメージである。そのため、X,YとZとのスケールの違いが問題になってくることもあるので要注意。
上のグラフをよく見ると、X軸・Y軸の値はデータの個数に相当していて、高さ方向のZ軸だけが-1から+1までの値をもっている。
{{x1,y1,z1},{x2,y2,z2},....}の3次元座標でデータを渡すのは別の関数が用意されている。

ScatterPlot3D[ ]をヘルプでみてみよう

ScatterPlot3D[ ]

[Graphics:HTMLFiles/Part1_694.gif]

応用例(数値地図データからマッターホルンを描く)

さて世の中には数値地図なるものが存在している。「数値地図」で検索すると様々なWebサイトが見つかるだろう。これは主としてGIS (Geographical Information System )関連の情報で、（緯度、経度、標高）といった地図の基本情報がデジタル化されたものだ。（緯度、経度、標高）ということは3次元データだ。そこでこれをもってきてMathematicaで表示しようと考えてみた。まずは数値地図の入手である。スイス地理院のサイトにはアルプスの地図のフリー版が置いてあるのでこれを使う。使うのはマッターホルンの地図である。

http://www.swisstopo.ch/en/digital/dhm25.htm

ここから、ftp://ftp.swisstopo.ch/pub/data/dhm/Matter.zip
というデータをダウンロードし、それを解凍するといくつものデータが得られるが25mメッシュに切ったテキストファイル、"mmmat25.xyz"を用いることにする。そして自分のホームディレクトリ以下の適当な場所にこれを格納しておく。Windowsであれば、マイドキュメント以下のどこかのフォルダに置いておけばよいだろう。そしてそのフォルダのパスを覚えておく。
次に、そのデータがあるフォルダ（ディレクトリ）を読み込み元のフォルダとして指定をしなければならないので、そのための関数、SetDirectory[ ]を用いる。

$SetDirectory["C:\\home\\ohgi\\Research\\2006\\MathBook\\ImportData"]$

$C:\\home\\ohgi\\Research\\2006\\MathBook\\ImportData$

ファイル入出力については以降の章で詳細に説明を加えるのでここではあまり深く考えずに自分の環境にあったようにフォルダを指定しておこう。
次にテキストデータ読み込みの関数ReadList[ ]を用いて用意されたデータを読み込む。X,Y,Zが1行のデータなので、{Number.Number,Number}と３つで1くくりのデータとして読み込む。

ReadListは、ファイルからデータを読む取るための関数であり、いくつものオプションにより読み込むファイルのフォーマットに対応している。データはX,Yがそれぞれ25mおきに81のメッシュに区切られているので、それを分割してさらにZ座標だけを取り出す。そのために次のような処理をいったん施す。やっていることを理解できるだろうか？

$General :: spell1 : スペル間違いの可能性があります．新規シンボル\"mmmatz\"はすでにあるシンボル\"mmmat\"に似ています．詳細$

ListPlot3D[ ]を実行する。

[Graphics:HTMLFiles/Part1_702.gif]

自分の計算機上で3次元地図が出来上がった。応用例を考えていてこの数値地図を思いついてから初めてこれを見たときには筆者自身も大いに感動した。色んな角度で見てみよう。後上空から見てみる。視点を変えるにはViewPointというオプションを変える。

[Graphics:HTMLFiles/Part1_705.gif]

標高地図はすでに学んだListContourPlot[ ]を使えばよい。

[Graphics:HTMLFiles/Part1_708.gif]

練習問題

問：マッターホルン地図の等高線地図を以下のように濃淡なしの等高線だけにして描くにはどうしたらよいだろうか？ ContourListPlotのオプションをじっくりと探してみて欲しい

[Graphics:HTMLFiles/Part1_710.gif]

グラフィックスのImport/Export

Export : グラフィックスの出力

今まで作成してきた全てのグラフィックスは、ファイルとして書き出すことが可能である。それには関数Export[ ]を使う。またグラフをファイル出力する際には、グラフィックスオブジェクトを引数として渡してやることが必要だ。マッターホルンの地図を画像ファイルにして保存してみよう。そうすればWebに載せて他人に見せることも出来る。まずは、出力されるグラフィックスをグラフィックスオブジェクトとして一度変数に格納しておく。

[Graphics:HTMLFiles/Part1_713.gif]

次にこれを,Export[ ]を使ってファイルに出力する。

JPEG, TIFF, AI(Illustrator Format), EPS, PNG, BMP,SVGなどたいていの画像フォーマットで保存可能である。その際、拡張子で勝手に判断してくれる。

Import : グラフィックスの入力

Export[ ]が出来るなら、逆も可能である。Mathematicaに画像などを読み込むことが出来る。読み込むときも拡張子で自動的に判断してくれる。これにはすでに出てきた関数、Import[ ]を用いる。

読み込んだグラフィックスはMathematica内では、グラフィックスオブジェクトとして格納される。従ってグラフィックスオブジェクトを表示する関数、Show[ ]を使うことで表示が可能である。

[Graphics:HTMLFiles/Part1_722.gif]

千葉県安房郡鋸南町の鋸山の日本寺にある日本最大の大仏だ。石像総高31メートル。実際に筆者が行って写真を撮ってきた。さてここでMathematicaのグラフィックス関数をつかってこれを加工してみよう。何をするかというと大仏さんに文字を書き込んでみる。

Text[ ]は後ほど説明するが、グラフィックスを操作するグラフィックス原始関数のひとつである。

[Graphics:HTMLFiles/Part1_727.gif]

このようにグラフィックスのなかに文字を書き込むことも自由にできる．あらかじめ作っておいたグラフに注釈を入れたりするにも便利である．

パッケージ関数の利用

様々なグラフが利用できることが分かったが、エクセルなどの表計算ソフトでデフォルトで用意されているいくつかのグラフがないことに気がついたかもしれない。例えば、棒グラフや円グラフなど。そういったグラフはパッケージになっていてこれを読み込むことでいつでも使用可能である。これらのグラフの関数はパッケージ、Graphics`Graphicsに収められている。これを読み込む。パッケージの読み込みはここで最初に出てきたが、どんなパッケージがあるのかを知りたいときには、ヘルプブラウザーから、「アドオンとリンク」から「標準パッケージ」を選択すると標準で読み込むことが出来るパッケージを確認することが出来る。

バッククォートに注意する。これでいくつかのGraphics Package関数たちが読み込まれた．では実際に使ってみよう．

BarChart[ ] : 棒グラフ

棒グラフは簡単だ。データはリストで用意する。

[Graphics:HTMLFiles/Part1_733.gif]

2つのリストを棒グラフで表示すると次のように色が変わり、2つの系列が表示される。

[Graphics:HTMLFiles/Part1_736.gif]

横方向の棒グラフは次の例のように，オプション，BarOrientation->Horizontal で指示する．

[Graphics:HTMLFiles/Part1_739.gif]

PieChart[ ] : 円グラフ

円グラフも同様に簡単である。同じくデータはリストで用意してこれを関数、PieChart[ ]に渡してやる。

[Graphics:HTMLFiles/Part1_742.gif]

PieChart[ ]の場合には、データを一つのリストで与える。そのリストの数値を全部合計したものを100[%]として百分率で示すのが、PieChartである。
任意の部分だけ切り取って表示するには、PieExplodedをつかう

[Graphics:HTMLFiles/Part1_744.gif]

見てわかるように,PiChart[ ]の場合には、グラフの開始地点は、角度０、すなわち３時の位置から始まっている。多くの円グラフが12時の位置から描き始めていることを考えると、ちょっと戸惑うかもしれない。

StackedBarChart[ ] : 積み上げグラフ

出費・経費などを表示するのに向くと思われる値の累積で色を違えて表示する積み上げグラフは，StackedBarChart[ ]である．(Mathematica Help Broswerより)

[Graphics:HTMLFiles/Part1_746.gif]

PercentileBarChart[ ] : 比率グラフ

値の割合を百分率で示す比率グラフは，PercentileBarChart[ ]である．(Mathematica Help Broswerより)

[Graphics:HTMLFiles/Part1_749.gif]

まだまだ様々なグラフが用意されているし、カスタマイズが自由に出来る。それがMathematicaの強みである。ここで紹介しなかったグラフについても本書の中で少ずつ紹介していく。また場合によっては自分でグラフを描く関数を作ることもできる．

グラフィックス原始関数 (Graphics Primitives)　とは

Mathematicaのグラフィックスは全て、グラフィックス原始関数（グラフィックスプリミティブ）を使って描かれる。これは、「点を描く」、「線を引く」といった基本的なことだけを行うものである。これらを組み合わせて様々なグラフを作るのである。そこでどうしても標準のグラフ関数では出来ないことをやりたい場合には、このグラフィックス原始関数を駆使することになる。

Line : 直線をひく

基本的な使い方はこうだ。まずはLine[ ]を例にしてみよう。Line[ ]は2点を結んだ線を引く。つまり2点の座標が必要である。そこで引数には2点の座標を引数にして渡してやる。今、(0,0)と(1,1)を結ぶ直線を描いてみよう。

返されたline1はまだグラフィックスオブジェクトではない。これをグラフィックスオブジェクトにするには、関数Graphics[ ]を用いる。それを表示するために， Show[ ]をこのグラフィックスオブジェクトを渡してやる。

[Graphics:HTMLFiles/Part1_754.gif]

グラフィックスオブジェクトには色や太さなども引数として与えられるので、

[Graphics:HTMLFiles/Part1_757.gif]

このように自由にカスタマイズできる

[Graphics:HTMLFiles/Part1_762.gif]

練習問題

問：3点、A(0,0), B(1,0), C(0,1)を結んで出来る三角形をグラフィックス原始関数を使って描け

問：任意の3点の2次元座標を与えると三角形を描く関数をグラフィックス原始関数を使って作れ

Point : 点を描く

点を描くにはその点の座標が分かればよい。

[Graphics:HTMLFiles/Part1_767.gif]

点が小さすぎて見えない。大きくしてみよう。

[Graphics:HTMLFiles/Part1_770.gif]

line1,line2と一緒に描こう

[Graphics:HTMLFiles/Part1_773.gif]

線を太くしたら気がつくのだが、後から描画したものが上書きされるために下に描かれているものは重なって見えなくなる。

その他のグラフィックス原始関数

ほかにも様々なグラフィックスプリミティブが用意されている。
Circle, Polygon, Rectangel, .....
用途に応じて使い分けることが必要だ。

練習問題

問：以下の属性データを表示するにはどのようなグラフの種類が適当か？実際にテストデータを作成してグラフを表示せよ。
(a)ある人の一生における身長の変遷
(b)ある政党の支持率を示す国民の割合
(c)収入に対する支出内訳（光熱費、食費、貯蓄費などなど）の年度ごとの変遷。1999年度、2000年度、2001年度…、というふうに。

ヘルプをよく読むこと! アドオンとリンク->標準パッケージ>Graphics->Graphics

問：グラフィックスプリミティブだけを使って、人形の顔（かかしの顔みたいなもので可）を作成せよ。円や点、線を駆使してみよ。まずは紙面に簡単な絵を描いてみて、その絵に必要なグラフィックスプリミティブを利用せよ。
ヘルプをよく読むこと! LineやPointでグラフィックスプリミティブを探すといろいろなものが見つかるはず。

[Graphics:HTMLFiles/Part1_776.gif]

Created by Mathematica (February 28, 2007)