５．クラスタリング手法の確立 (2001年度秋学期Ⅱ)
最大の難関である序列効果の問題が解決できたが、それに伴ってクラスタリング作業は振り出しに戻る。それならば、ここまでの手法においても実証的な裏づけに乏しかったいくつかの問題点も同時に片付けておきたいところである。
残された問題点とは以下の3点である。
<1>単純な支持度（回答数）によるレイヤー区分でよいのか
<2>各レイヤーのITEM数に明確な根拠がない
<3>アイテム間得点が信頼性に欠ける
そして、いずれも解決されるに至った。それぞれの処方箋を以下に示す。
<1>単純な支持度（回答数）によるレイヤー区分でよいのか
既述のように、iMapでは従来のような性差や世代差を前提としないため、層化抽出は用いていない。だが、その結果として、iMap.gr.jpのトップページにあるようにUSERの生年分布は1970年代生まれに偏ってしまった。これでは性差・世代差を前提とはしないといっても、年配層や若年層に支持されるITEMが過小評価されることは避けられない。
この問題に対する処方箋として、iMapでは以前から特化係数を用いてきた。わかりやすい例として「水島新司」を取り上げる。
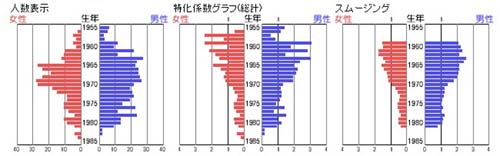
彼の生年・性別分布は上図左のような単なる人数表示では1960年代後半生まれのUSERにそのピークがあるように見える。しかし、これは見せかけの分布なのである。つまり、iMapのUSERにこの世代が多いという前提条件が実状を歪めているのである。
特化係数を用いると上図中央のようになり、さらにその移動平均をとることでスムージングを行うと右のようになる。これにより「水島新司」とは、1960年前半、あるいはそれよりもっと以前に生まれたUSERにおける支持が最も高い。と正しい判断が下されるわけである。
以上を参考にすれば、次のような補正方法を適用できる。すなわち、各ITEMの支持度を世代ごとにとり、全世代での平均をとって、それをランキングとみなすのである。
結果は以下の表のようになった。データクリーニング後にも増して、「手塚治虫」や「赤塚不二夫」といった、年配層に広く認知されている漫画家が上位に躍り出たことがわかる。全世代に高い認知度を誇る「藤子・F・不二雄」がクリーニング前に圧倒的な1位を獲得していた「あだち充」を抜いた点は、まさに序列効果の削除と平均支持度の相乗効果による大きな成果と考えられる。
|
未処理データのランキング
|
クリーニング後のランキング
|
平均支持度のランキング
|
||||
|
順位
|
ITEM名
|
USER数
|
ITEM名
|
USER数
|
ITEM名
|
平均支持度
|
|
1
|
あだち充 |
2162
|
あだち充 |
1693
|
藤子・F・不二雄 | 39.01% |
|
2
|
藤子・F・不二雄 |
1684
|
藤子・F・不二雄 |
1630
|
あだち充 | 37.10% |
|
3
|
鳥山明 |
1636
|
鳥山明 |
1584
|
鳥山明 | 35.56% |
|
4
|
一条ゆかり |
1581
|
高橋留美子 |
1400
|
手塚治虫 | 34.29% |
|
5
|
いがらしゆみこ |
1456
|
手塚治虫 |
1350
|
高橋留美子 | 31.53% |
|
6
|
高橋留美子 |
1441
|
一条ゆかり |
1336
|
さくらももこ | 30.64% |
|
7
|
さくらももこ |
1430
|
さくらももこ |
1327
|
一条ゆかり | 30.23% |
|
8
|
手塚治虫 |
1384
|
いがらしゆみこ |
1198
|
松本零士 | 28.65% |
|
9
|
秋本治 |
1199
|
藤子不二雄A |
1153
|
藤子不二雄A | 27.74% |
|
10
|
藤子不二雄A |
1188
|
松本零士 |
1127
|
いがらしゆみこ | 26.39% |
|
11
|
松本零士 |
1154
|
北条司 |
1124
|
石ノ森章太郎 | 25.01% |
|
12
|
北条司 |
1152
|
モンキー・パンチ |
978
|
赤塚不二夫 | 24.20% |
|
13
|
石ノ森章太郎 |
1136
|
石ノ森章太郎 |
951
|
モンキー・パンチ | 23.96% |
|
14
|
あさぎり夕 |
1049
|
秋本治 |
931
|
ちばてつや | 23.43% |
|
15
|
赤塚不二夫 |
1038
|
美内すずえ |
879
|
楳図かずお | 23.19% |
|
16
|
楳図かずお |
1000
|
ちばてつや |
856
|
水島新司 | 22.85% |
|
17
|
モンキー・パンチ |
995
|
あさぎり夕 |
851
|
北条司 | 22.82% |
|
18
|
浦沢直樹 |
982
|
楳図かずお |
848
|
秋本治 | 21.89% |
|
19
|
江口寿史 |
952
|
浦沢直樹 |
832
|
美内すずえ | 20.94% |
|
20
|
江川達也 |
926
|
赤塚不二夫 |
825
|
小林よしのり | 20.32% |
<2>各レイヤーのITEM数に明確な根拠がない
|
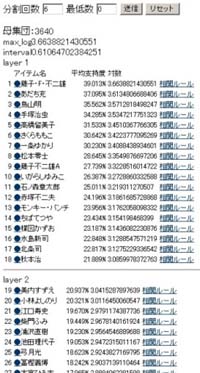
平均支持度の採用によってITEMランキングが変化し、各レイヤーに含まれるITEMにも入れ替わりが生じる。と、同時になぜ L1=35, L2=65, L3=100, L4=150というITEM数なのかという疑問に対して、漠然としか答えられない現状にも気づかざるを得ない。 ではどのようにすれば論理的なレイヤー区分が可能だろうか。そこで参考となるのが、大き過ぎるものと小さいものとの格差を縮小させる性質のある、対数という考え方である(10を底とした常用対数を考えればわかりやすい。1000⇒3, 100⇒2, 10⇒1である)。 ここでは、自然対数（e（2.71828…）が底）を用いた。平均支持度を自然対数化して、最大のものを基準に分割数を考えれば（対数の最大が10で分割数が5ならば、8・6・4・2 で5つに切れる）レイヤー区分を客観的に説明できるはずである。 分析の中心となるレイヤーをレイヤー3とし、それ以下はオルタナティブの次元だと仮定しているから、オルタナティブの次元にも3つのレイヤーが存在すると仮定すれば、レイヤー数の合計は6となる。 |
 |
<3>アイテム間得点が信頼性に欠ける
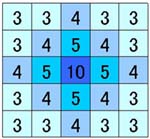右図のような点数化はあくまで恣意的である。それに加えて、夏休み中のクラスタリングでは、それぞれのクラスターが連結しない参考基準として、アイテム間得点の基準をL1=30,
L2=50, L3=70, L4=90と勝手に定めていた。これでは二重の恣意性の介在であり、基準の信頼性を証明するのは非常に難しい。
よって以下のように考える。
まず、同一レイヤー内におけるすべての組み合わせ数は
（アイテム数×アイテム数） － アイテム数
|
である(行と列は対称的であるから、これを2で割っても考え方は一緒である）。1度でも近くにプロットされたITEM同士は、右図のように、互いがクロスしたセルに点数が入ることになる。 点数化されなかった組み合わせがほとんどだが、これらをすべて0点と考えれば、以下のような分布図が描ける。 |
 |
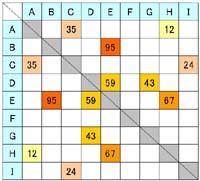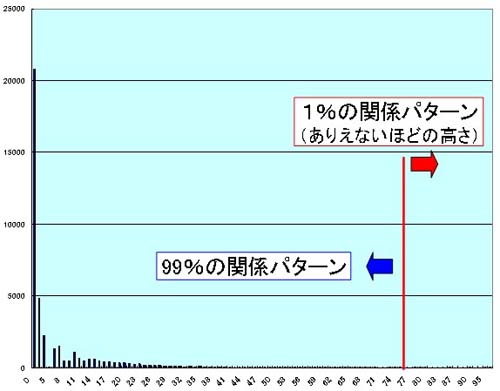
レイヤーの含むITEM数は違うから、その影響によって切れ目となる得点基準も異なる。結果は
レイヤー1：38（次点の27点で99.35％）
レイヤー2：63（次点の61点で99.05％ ）
レイヤー3：75（次点の74点で99.01％ ）
レイヤー4：77（次点の76点で99.04％ ）
であった。
ただし、下位のレイヤーになると、アイテム間得点が微妙に足りずにクラスタリングから漏れるケースが増えてくる。よって、下位のレイヤーでは作成されたクラスターをITEMと同等に扱うことで再度得点化を繰り返すこととした。
組み合わせ数は二乗の考え方であるから、その数はITEM数の増加によって指数関数的に増加する。このことは対数の考え方の裏返しなのだから、繰り返し数もそれに応じて、L1=1,
L2=2, L3=3, L4=4 とすればよい。
以上で「文化」(趣味)面におけるクラスタリングの手法はほぼ確立された。