Method4.クラスタリング
4-1. クラスタリングの必要性
レイヤー分割により、アイテムは認知度の近いもの同士に分類された。上位レイヤーならば、個別にアイテム1個1個のアソシエーション・ルール結果を参照することも可能だが、下位レイヤーに含まれるアイテム数は膨大であり、その手段は現実的ではない。よって数を縮約し、視覚的な構造把握を可能にする、クラスター分析を行いたい。
インプットデータとしては、「アイテム」と「ユーザ」とを行列にとり、クリックされた場合を1(True)、そうでない場合を0(False)とした、フラグ値によって構成されるテーブルを用意する。トランザクションのクロス表である、このようなスパースな疎行列を扱う場合、厳密解は期待できない。いやむしろ、サブカルチャー分析には多様な配置方法こそ望まれている。そこでクラスタリング技法としては、全体の平均(重心)や分散(共分散)に強く依存する固有値計算技法よりも、ニューラルネットワークを応用した技法が適していると考えられ、Kohonenネットワークの利用がベストであると判断した。
Kohonenネットワークは、以下の4タイプの中では、K-means法とも呼ばれる(4)に近い技法とされるが、ここでの命題は「Kクラスタイリング問題」(望ましいクラスター数が決まっている)ではないため、その点から比較してもKohonenネットワークの方が、より適合的である。
「クラスタリングのアルゴリズムとしては (1)階層的クラスタリング、(2)単純クラスタリング、(3)最大距離アルゴリズム、(4)K平均アルごリズム といったものが知られているが、どれも初期状態やパラメータに強く左右される手法である」 (武藤佳恭『ニューラルコンピューティング』コロナ社、1996、p.46)
4-2. Kohonenネットワークの限界克服
しかしKohonenネットワークは、ランダムシードの設定や隣接の値を変えるたびに異なるアウトプットがもたらされるため、"ブラックボックスである"とよく言われる。以下2文献から代表的な指摘を引用してみよう。
「ニューラル・ネットワークに対する長年の批判の一つは、それが「ブラックボックス」であり、解釈困難であり、その振る舞いや、なぜその結論に到達するかを説明できないということであった」 (ジョゼフ・P・ビーガス(Joseph P. Bigus)、社会調査研究所・日本IBM(訳)『ニューラルネットワークによるデータマイニング』日経BP、1997、p.130)
「ニューラルネットワークは、神秘的なブラックボックスと考えたほうがよい。私たちの意識の根元が神秘的なのと同様に、ニューラルネットワークも内部の働きは理解しづらい」 (マイケル・J・A・ベリー(Michael J. A. Berry)/ゴードン・リノフ(Gordon Linoff)、SASインスティチュート ジャパン・江原淳・佐藤栄作(訳)『データマイニング手法』海文堂、1999、p.212)
だが、後者のいう複雑性と柔軟性は、まさしく我々人間の思考に近いものであり、活用法さえ間違わなければ、サブカルチャーの現状を把握するのに、これほど適した技法はないように思われる。問題は、1回の試行によって最適解が得られるという、従来型発想に基づく誤認にこそあろう。そこで、行われるクラスタリングのすべてが正しいという仮定の下に、次なる「アイテム間得点」に基づくクラスタリング手法を考案した。
アイテム間得点とは、2つのアイテム同士の類似性を測る指標であり、0〜100の値を取り、値が大きいほど類似性が高いことを示す 。レイヤーごとに、以下の手順によって求められる。
アイテム間得点の算出方法
|
1
|
出力マップに幅10×長さ10の100セルを持たせ、Kohonenネットワークを実行する。 |
 |
|
2
|
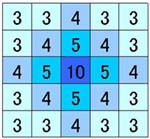
実行結果の全アイテムの座標を把握し、1つ1つ、別アイテムとの位置関係を右表のように得点化する。表の中心が基点であり、表の範囲外のアイテムとの得点はすべて0点である。 | |
|
3
|
ランダムシードの値を変え、同様の得点化を10回繰り返す。 | |
| 4 | アイテムのペアごとに得られる10回分の得点の総和を「アイテム間得点」とする。 |
このようにアイテム間得点を求めれば、初期値の違いに関わらず恒常的に近くにプロットされるアイテム同士の得点は高くなり、逆に偶然ある回だけ同一のセルにプロットされたようなアイテム同士の得点はトータルとして低くなる。この手法を用いれば、Kohonenネットワークのクラスタリング結果がもつ説明力は飛躍的に向上する。その後のクラスタリングにおいても、アイテム間得点を利用した様々な手法が考えられよう。それぞれのアイテムにおいて最も得点の高いアイテムを次々に結び付けていく凝集法における単一連結法のようなアプローチや 、全体における基準値以上の高得点を利用する上位水準などが、例として挙げられる。